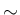
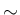 4. のうち、
多分 3. の漸化式ができれば、
あとのものは帰納法で示されるので、
まずは漸化式を求める。
それには、(3) に (1) を
適用すればよい。
4. のうち、
多分 3. の漸化式ができれば、
あとのものは帰納法で示されるので、
まずは漸化式を求める。
それには、(3) に (1) を
適用すればよい。
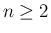 に対して、
(1) に (3) を代入すると、
に対して、
(1) に (3) を代入すると、
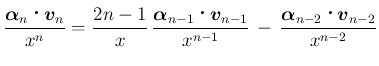
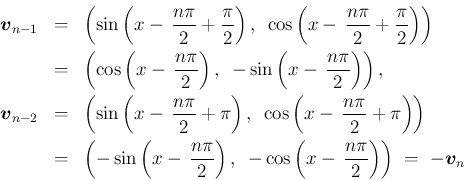
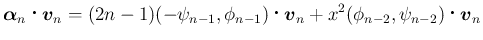
 ,
,  に対する漸化式は、
となる。この漸化式と (4) により、
すべての
に対する漸化式は、
となる。この漸化式と (4) により、
すべての 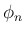 ,
, 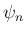 が確定する。
が確定する。
次は、この漸化式を用いて、3 節最後の 1., 2., 4. を 示していこう。
まずは 1. の次数であるが、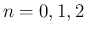 では成立している。
(6) から、
では成立している。
(6) から、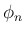 の方 (1 本目) は、
帰納法で考えれば右辺は
の方 (1 本目) は、
帰納法で考えれば右辺は 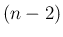 次式と
次式と 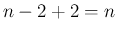 次式の和になるので、
確実に
次式の和になるので、
確実に 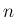 次式となるが、問題は
次式となるが、問題は 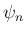 の方 (2 本目) で、
これは右辺が
の方 (2 本目) で、
これは右辺が 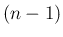 式と
式と 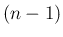 次式の和なので、
最高次の係数が 0 でないことをちゃんと示す必要がある。
次式の和なので、
最高次の係数が 0 でないことをちゃんと示す必要がある。
よって、1. をさらに詳しく、
として、この係数は、
の係数が
である高々
次式、
は、
の係数が
である高々
次式 (
)
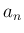 ,
, 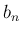 が 0 にならないことを示す。
が 0 にならないことを示す。
漸化式 (6) より、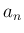 ,
, 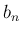 については、
以下の漸化式が成り立つことがわかる。
については、
以下の漸化式が成り立つことがわかる。
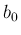 は
は 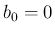 とするが、
こうすれば、(7) はすべての
とするが、
こうすれば、(7) はすべての 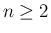 に対して
成立する。
に対して
成立する。
(4) により、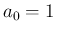 ,
, 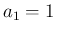 なので、
なので、
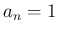 がすべての
がすべての 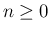 に対して成り立つ。
に対して成り立つ。
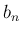 は、
は、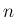 が偶数、奇数で分けると
が偶数、奇数で分けると 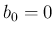 ,
, 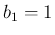 より、
より、
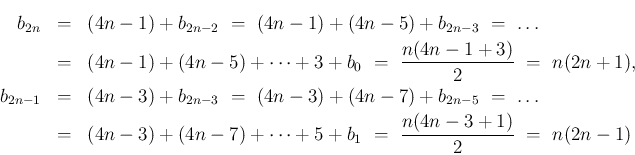
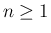 では
では 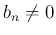 が保証され、
よってこれで 1. が示されたことになる。
が保証され、
よってこれで 1. が示されたことになる。
奇関数、偶関数の関係 2. は、(6) と 帰納法で容易に示すことができるので、説明は省略する。
最後に、4. の、ノイマン関数に対する (5) を示す。
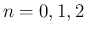 に対しては、(5) は
成り立っているから、あとは帰納法を用いる。
すなわち、(5) が
に対しては、(5) は
成り立っているから、あとは帰納法を用いる。
すなわち、(5) が 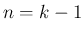 まで
成り立っているとする (
まで
成り立っているとする (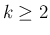 ) と、
) と、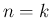 に対しては、
漸化式 (1) より、
に対しては、
漸化式 (1) より、
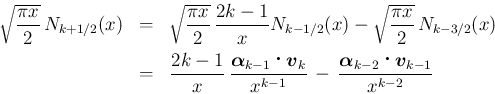
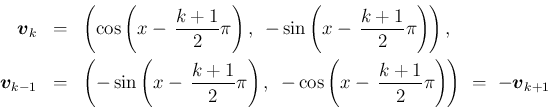
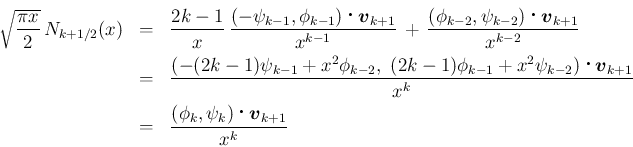
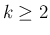 に対して言えるので、
帰納法により (5) がすべての
に対して言えるので、
帰納法により (5) がすべての 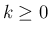 に
対して示されたことになる。
に
対して示されたことになる。
竹野茂治@新潟工科大学