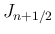
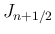 ,
, 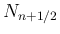 は、いずれも
は、いずれも
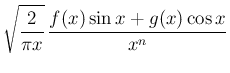
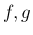 は多項式の形になることがわかる。
よってあとはこの
は多項式の形になることがわかる。
よってあとはこの 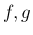 の部分を求めればよいことになる。
の部分を求めればよいことになる。
2 節の結果から、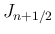 に
対する
に
対する 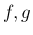 (
(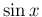 ,
, 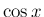 の係数) は、
の係数) は、
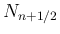 に対する
に対する  (
(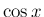 ,
, 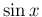 の係数) と
符号の違い程度であることが予想でき、
また、
の係数) と
符号の違い程度であることが予想でき、
また、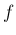 と
と 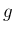 の次数は一つ違っていて、
その次数の高い方も、
の次数は一つ違っていて、
その次数の高い方も、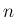 の増加に対して入れ替わると予想される。
よって、
の増加に対して入れ替わると予想される。
よって、
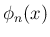 が次数の高い (と予想される) 方である。
が次数の高い (と予想される) 方である。
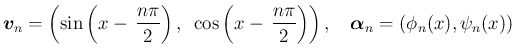
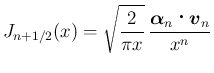
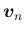 の最初の 4 つは
の最初の 4 つは
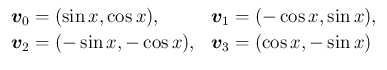
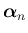 の最初の 3 つを見てみると、
2 節の計算より、
となることがわかる。
の最初の 3 つを見てみると、
2 節の計算より、
となることがわかる。
一方、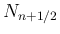 の
の 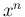 の分子の
の分子の
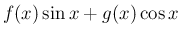 の部分は、
丁度
の部分は、
丁度
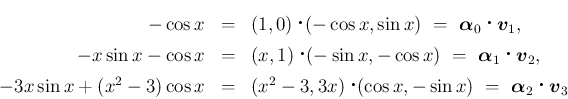
ここまでをまとめて、今後以下のことを示すことにする。
 は
は 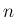 次式、
次式、
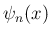 は
は 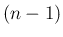 次式 (
次式 (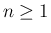 のとき)
のとき)
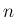 が奇数の場合は
が奇数の場合は 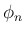 は奇関数、
は奇関数、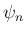 は偶関数で、
は偶関数で、
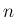 が偶数の場合は
が偶数の場合は 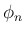 は偶関数、
は偶関数、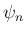 は奇関数
は奇関数
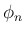 と
と 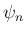 に関する微分のない漸化式を得ること
に関する微分のない漸化式を得ること
竹野茂治@新潟工科大学