3 単純な設定での考察
簡単に、毎回同じ金額の物品を購入することにして、
以下のように設定する。
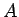 = 毎回購入する税込代金 (
= 毎回購入する税込代金 (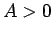 , 例えば
, 例えば 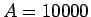 円)
円)
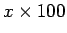 % = 代金に対してポイントがつく割合 (
% = 代金に対してポイントがつく割合 (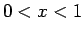 , 例えば
, 例えば 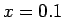 )
)
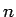 = 購入回数
= 購入回数
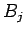 =
= 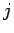 回目の現金での支払い額
回目の現金での支払い額
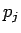 =
= 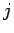 回目の支払い後のポイント数
回目の支払い後のポイント数
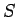 =
= 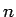 回の支払い総額 (
回の支払い総額 (
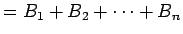 )
)
ポイントの使用方法は、
- 使用方法 1.
- 毎回全部のポイントを支払いに使用する
- 使用方法 2.
- 支払い額を越えるまでたまったら使用する
など色々あると思うが、今回はこの 2 種類を考える。
まず、使用方法 1. を考える。
この場合は規則的なので、一般的な式で考察する。
初回の買物ではポイントは 0 なので、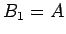 円支払って、
その後に
円支払って、
その後に 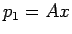 ポイントもらえることになる。
なお、本来ポイントは、小数以下を切り上げにするところが多いようであるが、
今は端数は小数のまま考える (整数化しない) こととする。
ポイントもらえることになる。
なお、本来ポイントは、小数以下を切り上げにするところが多いようであるが、
今は端数は小数のまま考える (整数化しない) こととする。
2 回目の買物ではポイントを使用して、現金は
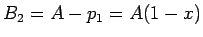 円支払い、
円支払い、
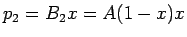 ポイントがつくことになる。
ポイントがつくことになる。
以下同様で、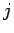 回目の買物では
回目の買物では 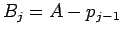 円の現金を支払い、
円の現金を支払い、
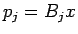 ポイントがつく。
つまり、
ポイントがつく。
つまり、
という漸化式が成り立つので、
より 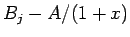 が等比数列になるので、
が等比数列になるので、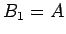 より
より
なので、
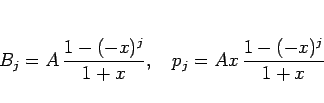 |
(1) |
となる。
なお、これは 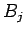 を順に書き下して、
を順に書き下して、
及び等比数列の和の公式から導くこともできる。
これは確かに複利に似た構造だが (ルール 5. に起因)、
公比は 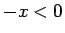 なので、複利とはやや異なる。
なので、複利とはやや異なる。
そして、支払い代金の合計 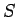 は
は
より、
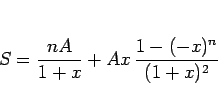 |
(2) |
となるから、ポイントにより値引きされた総額は
となり、結局ポイントの使用方法 1. での値引き率 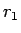 は
は
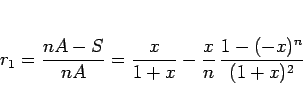 |
(3) |
となる。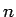 が大きく、
が大きく、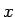 が小さい場合は、
が小さい場合は、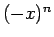 はほぼ 0 に近く、
よってこれは
はほぼ 0 に近く、
よってこれは
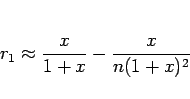 |
(4) |
で近似でき、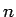 がさらに大きければ右辺第 2 項も無視して、
がさらに大きければ右辺第 2 項も無視して、
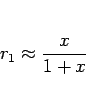 |
(5) |
と近似できることになる。これは当然 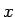 より小さく、
例えば
より小さく、
例えば 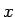 が 10% であれば、
が 10% であれば、
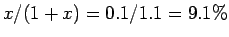 程度で、
(4) の方はそれよりもさらに (少しばかり) 小さい。
程度で、
(4) の方はそれよりもさらに (少しばかり) 小さい。
なお、値引き総額に最終ポイント数も入れた金額を得した金額と考えれば、
その総額は
となり、値引き率 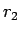 は
は
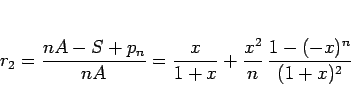 |
(6) |
となり 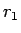 より少し大きくなる。
しかし、この第 2 項は
より少し大きくなる。
しかし、この第 2 項は 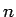 が大きく、
が大きく、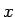 が小さければやはり
第 1 項に比べて無視できるほど小さな値となるので、
(5) とあまり変わらない。
が小さければやはり
第 1 項に比べて無視できるほど小さな値となるので、
(5) とあまり変わらない。
なお、ここまでの議論は、金額の小数以下の端数も含めた計算であるが、
本来ポイントや代金には小数値を考えない。
その場合上の計算の 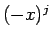 の部分はあるところから先は端数となり、
よって実際にはこのような式にはならないことにも注意する。
の部分はあるところから先は端数となり、
よって実際にはこのような式にはならないことにも注意する。
竹野茂治@新潟工科大学
2018年2月15日
![]() 円支払って、
その後に
円支払って、
その後に ![]() ポイントもらえることになる。
なお、本来ポイントは、小数以下を切り上げにするところが多いようであるが、
今は端数は小数のまま考える (整数化しない) こととする。
ポイントもらえることになる。
なお、本来ポイントは、小数以下を切り上げにするところが多いようであるが、
今は端数は小数のまま考える (整数化しない) こととする。
![]() 円支払い、
円支払い、
![]() ポイントがつくことになる。
ポイントがつくことになる。
![]() 回目の買物では
回目の買物では ![]() 円の現金を支払い、
円の現金を支払い、
![]() ポイントがつく。
つまり、
ポイントがつく。
つまり、
![]() は
は
![]() の部分はあるところから先は端数となり、
よって実際にはこのような式にはならないことにも注意する。
の部分はあるところから先は端数となり、
よって実際にはこのような式にはならないことにも注意する。