4 6 次方程式への帰着
今、例えば 2 重根号
![\begin{displaymath}
x=\sqrt[3]{3+\,\frac{11}{9}\sqrt{6}}\end{displaymath}](img82.gif) |
(20) |
を外すために、普通にこの 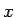 が満たす代数方程式を求めると、
(20) をまず 3 乗して
が満たす代数方程式を求めると、
(20) をまず 3 乗して
となり、3 を移項して 2 乗すれば
が得られ、よって有理数係数の 6 次方程式
が得られる。
もし、この方程式の 2 次式の因数をなんらかの方法で見つけて
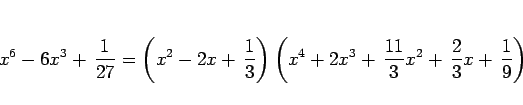 |
(21) |
と因数分解とし、そして 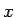 が
が
の解で、よって
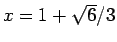 であることを知る方法があれば、
このような手順でも 2 重根号を外すことができるかもしれないが、
この道筋には、以下のような難点がある。
であることを知る方法があれば、
このような手順でも 2 重根号を外すことができるかもしれないが、
この道筋には、以下のような難点がある。
- 6 次式の 2 次因数を見つけることが困難
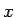 がその 2 次方程式の解であることを示すことが困難
がその 2 次方程式の解であることを示すことが困難
前者も易しくはないが、
後者は 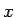 が残りの 4 次方程式の解ではないことを示す必要があり、
(21) の場合には
その 4 次方程式が実数解を持たないことから示されるのであるが、
それをちゃんと示すのは易しくない。
が残りの 4 次方程式の解ではないことを示す必要があり、
(21) の場合には
その 4 次方程式が実数解を持たないことから示されるのであるが、
それをちゃんと示すのは易しくない。
よって、この 6 次方程式を経由する方法は良い方法ではなく、
次節では 3 節で紹介した 3 次方程式の解を
利用する方法を紹介する。
竹野茂治@新潟工科大学
2018-03-02