3 3 次方程式の解法
本節では、3 次方程式の一般的な解法 (解の公式) を紹介する。
本稿では、
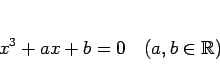 |
(8) |
の形の 3 次方程式についてのみ説明するが、より一般の
の形の 3 次方程式を (8) の形に
帰着させるのは難しいことではない (例えば [1] 参照)。
また、係数 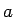 ,
, 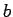 は本節では実数とするが、
その他の節では原則有理数のみを扱う。
は本節では実数とするが、
その他の節では原則有理数のみを扱う。
(8) において 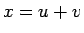 として代入すると、
として代入すると、
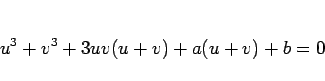 |
(9) |
が得られる。ここから
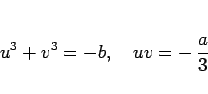 |
(10) |
を満たす 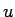 ,
, 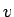 を求めて
を求めて 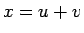 とする、
というのが一般的な 3 次方程式の解法 (解の公式) である。
とする、
というのが一般的な 3 次方程式の解法 (解の公式) である。
なお、(9) から (10) が
成り立たなければいけないわけではないが、
(10) が成り立てば (9) は
当然成り立つ。そして、(10) から
3 つの解はすべて得られる、という仕組みになっている。
また、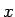 ,
, 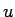 ,
, 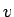 は一般には複素数である。
は一般には複素数である。
(10) より、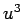 ,
, 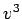 は、2 次方程式
は、2 次方程式
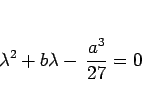 |
(11) |
の解となる。この方程式の判別式
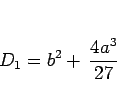 |
(12) |
の符号により、場合分けして考える。
まずは 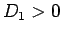 の場合であるが、
この場合 (11) は異なる 2 つの実数解
の場合であるが、
この場合 (11) は異なる 2 つの実数解
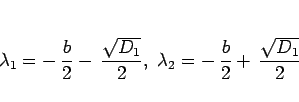 |
(13) |
を持つ。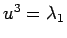 ,
, 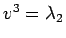 と対応させれば、
と対応させれば、
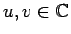 より
より
![\begin{displaymath}
u
=\sqrt[3]{\lambda_1},
\sqrt[3]{\lambda_1}\,\omega,
\sq...
...},
\sqrt[3]{\lambda_2}\,\omega,
\sqrt[3]{\lambda_2}\,\omega^2\end{displaymath}](img41.gif) |
(14) |
となる。ここで、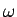 は
は
で、
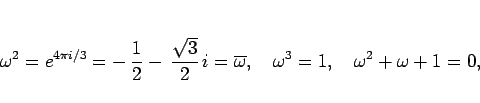 |
(15) |
を満たす。
なお、(11) の解と係数の関係より、
なので、
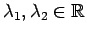 より
より
となるから、
(14) の 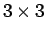 の
組み合わせのうち、(10) の
の
組み合わせのうち、(10) の 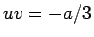 を
満たすものは
を
満たすものは
の 3 種類であることがわかる。これにより、
3 次方程式 (8) の解は
![\begin{displaymath}
x = u+v = \sqrt[3]{\lambda_1}+\sqrt[3]{\lambda_2},
\hspace...
...5zw}\sqrt[3]{\lambda_1}\,\omega^2 + \sqrt[3]{\lambda_2}\,\omega\end{displaymath}](img51.gif) |
(16) |
と表される。最初のものは実数であるが、
![$\sqrt[3]{\lambda_1}<\sqrt[3]{\lambda_2}$](img52.gif) より後の 2 つは虚数となる。
よって、
より後の 2 つは虚数となる。
よって、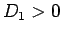 の場合は、方程式 (8) は 1 つの実数解と 2 つの虚数解を持つことになる。
の場合は、方程式 (8) は 1 つの実数解と 2 つの虚数解を持つことになる。
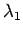 ,
, 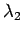 は (13) のように平方根で表されるので、
一般にはこの解には (1) の形の 2 重根号が
含まれることになる (
は (13) のように平方根で表されるので、
一般にはこの解には (1) の形の 2 重根号が
含まれることになる (
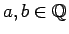 ,
,
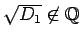 の
場合)。
の
場合)。
次は 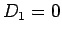 の場合であるが、この場合は
の場合であるが、この場合は
となり、また (15) より
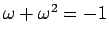 なので、
解は
なので、
解は
の 2 つであることがわかる (後者は重解)。
この場合は解には 2 重根号は現れない。
最後は 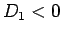 の場合であるが、この場合
の場合であるが、この場合 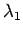 ,
, 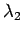 は
は
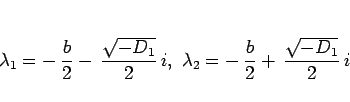 |
(17) |
の虚数となる。つまり 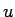 ,
, 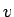 は「虚数の 3 乗根」となるが、
それを認めれば、形式的に (16) と同じ式が
解となる。以下でこの虚数の 3 乗根について少し説明し、
その式の意味をもう少し明らかにする。
は「虚数の 3 乗根」となるが、
それを認めれば、形式的に (16) と同じ式が
解となる。以下でこの虚数の 3 乗根について少し説明し、
その式の意味をもう少し明らかにする。
虚数 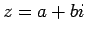 (
(
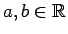 ,
, 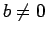 ) に対して、
) に対して、
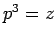 となる複素数
となる複素数 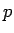 を
を 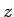 の 3 乗根と呼ぶが、
その実部と虚部を
の 3 乗根と呼ぶが、
その実部と虚部を 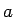 ,
, 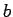 で表すのは難しい。
で表すのは難しい。
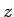 を極座標表示して
を極座標表示して
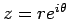 (
(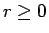 ) とすると、
) とすると、
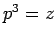 となる
となる 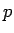 は
は
と表される。これが 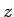 の 3 乗根であり、複素数では 3 つあることになる。
の 3 乗根であり、複素数では 3 つあることになる。
今、(17) の 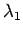 を
を
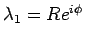 (
(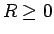 ) と極座標表示すると、
(12) より
) と極座標表示すると、
(12) より
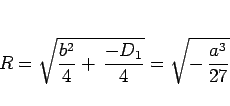 |
(18) |
となる。また、 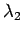 は
は 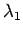 の共役であるから
の共役であるから
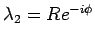 となり、よって
となり、よって 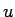 ,
, 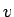 はそれぞれ
はそれぞれ
となる。この中で (10) の 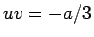 となるのは、
(18) より
となるのは、
(18) より
![$\sqrt[3]{R}=\sqrt{-a/3}$](img77.gif) なので、
なので、
の 3 種類となる。これらはいずれも 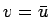 となっているので、結局
となっているので、結局
![\begin{displaymath}
x = u+v = 2\sqrt[3]{R}\,\cos\frac{\phi}{3},
\hspace{0.5zw}...
...+2\pi}{3},
\hspace{0.5zw}2\sqrt[3]{R}\,\cos\frac{\phi+4\pi}{3}\end{displaymath}](img80.gif) |
(19) |
のように表されることになる。
よって、この 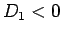 の場合は 3 つの実数解が得られる。
の場合は 3 つの実数解が得られる。
なお、この 3 つの実数解 (19) については、
最初から方程式を 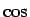 の 3 倍角の公式と比較して
解を三角関数 (と逆三角関数) で表現する方法もあるが ([1] 参照)、それは結果的に (19) と
ほぼ同等である。
の 3 倍角の公式と比較して
解を三角関数 (と逆三角関数) で表現する方法もあるが ([1] 参照)、それは結果的に (19) と
ほぼ同等である。
本稿で必要となる、「実数の範囲での 3 乗根と平方根の 2 重根号」
が現れるのは、結局 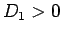 の場合の唯一の実数解となる。
の場合の唯一の実数解となる。
竹野茂治@新潟工科大学
2018-03-02
![]() として代入すると、
として代入すると、
![]() ,
, ![]() ,
, ![]() は一般には複素数である。
は一般には複素数である。
![]() ,
, ![]() は、2 次方程式
は、2 次方程式
![]() の場合であるが、
この場合 (11) は異なる 2 つの実数解
の場合であるが、
この場合 (11) は異なる 2 つの実数解
![]() ,
, ![]() は (13) のように平方根で表されるので、
一般にはこの解には (1) の形の 2 重根号が
含まれることになる (
は (13) のように平方根で表されるので、
一般にはこの解には (1) の形の 2 重根号が
含まれることになる (
![]() ,
,
![]() の
場合)。
の
場合)。
![]() の場合であるが、この場合は
の場合であるが、この場合は
![]() の場合であるが、この場合
の場合であるが、この場合 ![]() ,
, ![]() は
は
![]() (
(
![]() ,
, ![]() ) に対して、
) に対して、
![]() となる複素数
となる複素数 ![]() を
を ![]() の 3 乗根と呼ぶが、
その実部と虚部を
の 3 乗根と呼ぶが、
その実部と虚部を ![]() ,
, ![]() で表すのは難しい。
で表すのは難しい。
![]() を極座標表示して
を極座標表示して
![]() (
(![]() ) とすると、
) とすると、
![]() となる
となる ![]() は
は
![]() を
を
![]() (
(![]() ) と極座標表示すると、
(12) より
) と極座標表示すると、
(12) より
![]() の 3 倍角の公式と比較して
解を三角関数 (と逆三角関数) で表現する方法もあるが ([1] 参照)、それは結果的に (19) と
ほぼ同等である。
の 3 倍角の公式と比較して
解を三角関数 (と逆三角関数) で表現する方法もあるが ([1] 参照)、それは結果的に (19) と
ほぼ同等である。
![]() の場合の唯一の実数解となる。
の場合の唯一の実数解となる。