

Next: 4 の計算
Up: ある定積分について
Previous: 2 置換積分と部分分数分解
(PDF ファイル: kusa1.pdf)
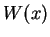 の式のうち、
の式のうち、
などは (0 次式)/(2 次式) なのでちゃんと収束しますので、
これをまず分けます。
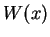 ,
, 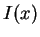 は有限なので、
は有限なので、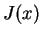 も一応有限ですが、
これは 2 つに分けるのは危険です。
も一応有限ですが、
これは 2 つに分けるのは危険です。
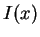 は、
は、
と一つにしてみると分かりますが、被積分関数は偶関数なので
とでき、よって
となります (この計算はすべて有限の範囲なので問題はありません)。
分母をそれぞれ
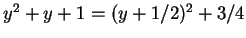 ,
,
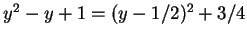 と標準変形し、
と標準変形し、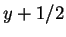 ,
, 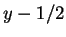 を
を 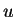 と置換積分すると
(このために
と置換積分すると
(このために 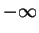 から
から 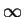 の積分に変えてあります)
の積分に変えてあります)
となります。最後の式には公式 (2) を使いました。
後は残りの 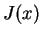 の計算です。
の計算です。


Next: 4 の計算
Up: ある定積分について
Previous: 2 置換積分と部分分数分解
Shigeharu TAKENO
2003年 11月 27日
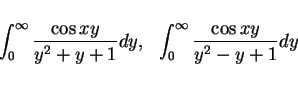
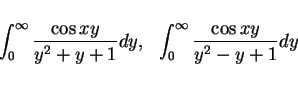
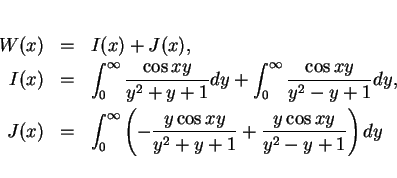
![]() は、
は、
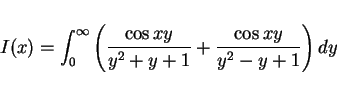
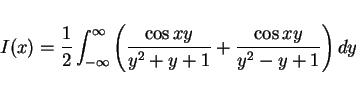
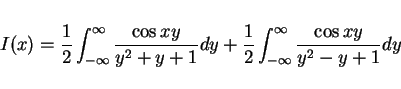
![]() ,
,
![]() と標準変形し、
と標準変形し、![]() ,
, ![]() を
を ![]() と置換積分すると
(このために
と置換積分すると
(このために ![]() から
から ![]() の積分に変えてあります)
の積分に変えてあります)
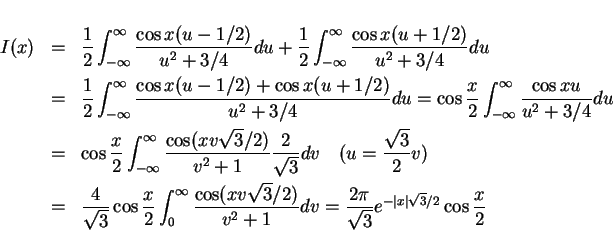
![]() の計算です。
の計算です。