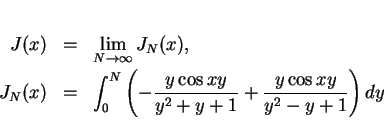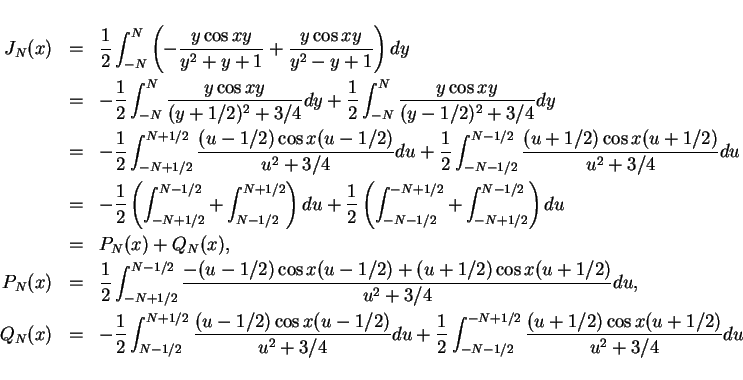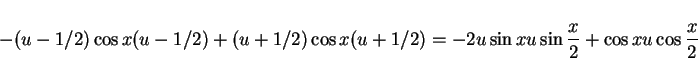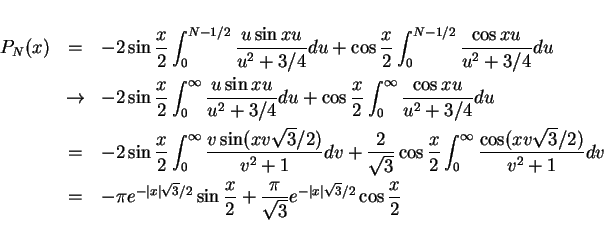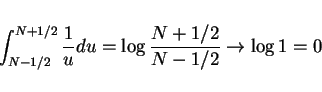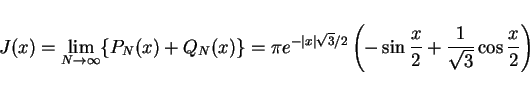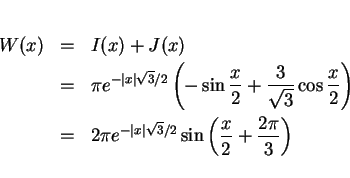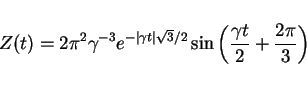

Next: 参考文献
Up: ある定積分について
Previous: 3 有限部分の引き算
(PDF ファイル: kusa1.pdf)
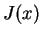 自体は前に述べたようにかなり微妙なので、広義積分の極限を取る前の式で
考えてみることにします。
自体は前に述べたようにかなり微妙なので、広義積分の極限を取る前の式で
考えてみることにします。
とします。この 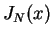 を 2 つに分けて
を 2 つに分けて  のようにそれぞれの分母を
標準変形して置換積分してみます。まず、
のようにそれぞれの分母を
標準変形して置換積分してみます。まず、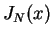 の被積分関数が
偶関数であることに注意して
の被積分関数が
偶関数であることに注意して 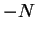 から
から 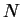 までの積分に直してからそれを行います。
までの積分に直してからそれを行います。
さてこの 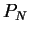 ですが、加法定理により
ですが、加法定理により
となり、偶関数なので 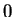 から
から 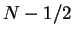 の積分に直すと
の積分に直すと
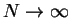 に対し
に対し
となります。後の残りの 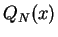 ですが、実はこれは 0 に収束します。
それは、
ですが、実はこれは 0 に収束します。
それは、
とほぼ同様に示すことができます。
よって、結局
となります。故に
となり、
となるようです。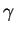 も
も 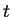 も正ならば、絶対値はなくても結構です。
も正ならば、絶対値はなくても結構です。
多分、元の式がきれいな形なのでそう面倒ではなくうまく求めることができました。


Next: 参考文献
Up: ある定積分について
Previous: 3 有限部分の引き算
Shigeharu TAKENO
2003年 11月 27日
![]() 自体は前に述べたようにかなり微妙なので、広義積分の極限を取る前の式で
考えてみることにします。
自体は前に述べたようにかなり微妙なので、広義積分の極限を取る前の式で
考えてみることにします。