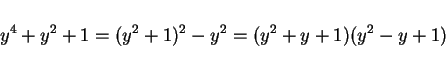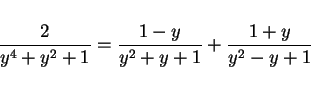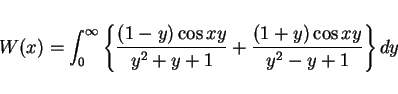

Next: 3 有限部分の引き算
Up: ある定積分について
Previous: 1 はじめに
(PDF ファイル: kusa1.pdf)
まず、置換積分と部分分数分解を行います。
なお、元の式 (1) は分母が 4 次式、分子は有限な関数
なので、ちゃんと積分は有限な値に収束します。
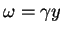 とすると、
とすると、
とすることができます。以後この 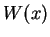 を考えます。
を考えます。
分母 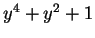 は
は
と因数分解され、よって 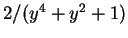 を部分分数分解すると
を部分分数分解すると
となります (計算は略)。ということで
となるのですが、この和をそれぞれの積分に分けることが可能かどうかは
実は微妙です。
それは 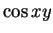 を除くといずれも (1 次式)/(2 次式) で、その広義積分は
一般には発散してしまうからで、しかし三角関数がつくと収束する場合もあり
(例えば (3) のように) かなり微妙です。
よって、有限な値をそっと引いて行くことにします。
を除くといずれも (1 次式)/(2 次式) で、その広義積分は
一般には発散してしまうからで、しかし三角関数がつくと収束する場合もあり
(例えば (3) のように) かなり微妙です。
よって、有限な値をそっと引いて行くことにします。


Next: 3 有限部分の引き算
Up: ある定積分について
Previous: 1 はじめに
Shigeharu TAKENO
2003年 11月 27日
![]() とすると、
とすると、
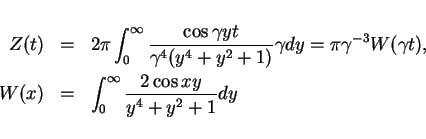
![]() は
は