9 他の硬貨系について
4 節で述べたように、これまでに見てきた命題は、
通常の 1 円、5 円、10 円、...の硬貨系 (5-2 硬貨系と呼ぶ) 以外の (10) の形の硬貨系でも成り立つ。
例えば、1 円、2 円、4 円、8 円、...(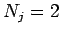 ) の 2 進数の硬貨系等の
) の 2 進数の硬貨系等の
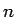 進数の硬貨系、
あるいは、12 進数を基本とした 6-2 硬貨系 (1 円、6 円、12 円、72 円、...) や
3-4 硬貨系 (1 円、3 円、12 円、36 円、...) なども作ることができる。
進数の硬貨系、
あるいは、12 進数を基本とした 6-2 硬貨系 (1 円、6 円、12 円、72 円、...) や
3-4 硬貨系 (1 円、3 円、12 円、36 円、...) なども作ることができる。
例えばアメリカのように、基本的に 5-2 硬貨系だけれども、
基本となる額の 1/4 硬貨 (25 セント硬貨) を入れているところもある。
それは、実際には冗長 (表現が一意にならない) でややこしいのだが、
便利な場合もあるらしい。
なお、日本の 5-2 硬貨系だと 25 円硬貨を入れると冗長で一意性がなくなる
が、例えば 10 円硬貨等を除いて、
- 1 円、5 円、25 円、50 円、100 円、500 円
- 1 円、5 円、25 円、50 円、250 円、500 円
のようにすれば一意性のある硬貨系となる。
さらに、イギリス (やユーロ) では、歴史的な経緯もあるらしいが、
通常の 5-2 系に 2 ペンスや 20 ペンスなどの硬貨もあり、
これも冗長である。例えば 1 円、2 円、5 円を考えると、
1 円は 1 枚でいいが (2 枚あると冗長)、
2 円は 4 円を表現するためには 2 枚なければいけない。
しかし、そうすると 5 円が 2 円 2 枚と 1 円 1 枚でも
表現されてしまうことになる。
さて、2 進数硬貨系などは、10 進数と 2 進数の変換をやらないといけないので、
とても実用にはならないと思うかもしれないが、
もし硬貨系が最初から 2 進硬貨系であれば、
例えば両者での数字の併記であるとか、
金額の計算には 10 進数を使わない等、
2 進と 10 進の変換をやらずに生活する工夫がなされているはずだろう。
だから、変換が面倒だろうから 2 進硬貨系はありえない、
と考えるのは早計だと思う。
2 進硬貨系だと、1000 円未満の数字を表現するには、
- 1、2、4、8、16、32、64、128、256、512
の 10 種類の硬貨が必要になる。これも大変だと思うかもしれないが、
2 進硬貨系では各硬貨は 2 枚以上持つ必要はなく、
それぞれ 1 枚だけあればすべての金額が表現できる。
つまり、財布の中の最大小銭枚数は 10 枚で済むことになる。
一方、通常の 5-2 系では、1 円、10 円、100 円は最大 4 枚、
5 円、50 円、500 円は最大 1 枚必要だから最大で合計 15 枚となり、
2 進硬貨系よりむしろ 5-2 系の方が財布がふくらみやすいことになる。
ついでに他の硬貨系についても 1000 円未満の最大枚数を見てみると、
- 3 進硬貨系: 1, 3, 9, 27, 81, 243, 729
7 種類で、243 円までは 2 枚必要、729 円硬貨は 1 枚でよいので、
最大
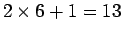 枚。
枚。
- 6-2 硬貨系: 1, 6, 12, 72, 144, 864
6 種類で、1 円、12 円、144 円は 5 枚、6 円、72 円、864 円は 1 枚なので
最大
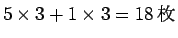
- 3-4 硬貨系: 1, 3, 12, 36, 144, 432
6 種類で、1 円、12 円、144 円は 2 枚、3 円、36 円は 3 枚、
432 円は 1 枚でよいので、最大
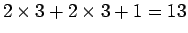 枚。
枚。
- 1 円、5 円、25 円、50 円、100 円、500 円:
1 円、5 円、100 円が 4 枚、25 円、50 円、500 円は 1 枚なので、
最大
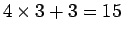 枚。
枚。
- 1 円、5 円、25 円、50 円、250 円、500 円:
1 円、5 円、50 円が 4 枚、25 円、250 円、500 円は 1 枚なので、
最大
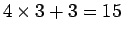 枚。
枚。
- 10 進系: 1, 10, 100
3 種類だがそれぞれ最大 9 枚なので 27 枚。
これを見ても、2 進硬貨系の 10 枚が少ないことがわかる。
もちろん、現在の 10 進数の日常から 2 進硬貨系に切りかえるのは
ほぼ不可能であるが、それなりに優れたところもあるように思う。
ちなみに、5-2 系の逆の 2-5 系 (1, 2, 10, 20, 100, 200 円硬貨) の場合も
最大は 15 枚となるし、
例えば 5 円玉だけを 2 円玉に変えるといった場合も同じになるが、
便利さや計算しやすさ、また平均的な小銭の枚数などには、
もしかしたら違いが出てくるかもしれない。
1 円玉を 1 枚作るのに、実際は 1 円以上必要だと何かで見たような気がするが、
もしそうだとすると、5 円玉の代わりに 2 円玉を使うようにすると、
1 円玉の流通量はずっと少なくすることができるだろう。
竹野茂治@新潟工科大学
2014年11月19日