これは、3 節と同じ 1 から 7 までの数字でいうと、 次のようなことを行う方法である。
| ■ | ■ | ||
| ■ | ■ |
| ■ | ■ | ||
| ■ | ■ |
| ■ | ■ | ■ | ■ |
| 9 | 15 | 24 | |
| 8 | 42 | 4 | 1 |
| 42 | ■ | 24 | ■ |
| 9 | ■ | 1 | ■ |
| 4 | 24 | ■ | ■ |
| 15 | 1 | ■ | ■ |
| 1 | 4 | 8 | 42 |
| ■ | ■ | ■ | ■ |
ゲームを行うときは、最初に 4 枚目のカードを見せ、 その 7 つの数字から一つを覚えてもらう。 そして、1 枚目、2 枚目、3 枚目のカードに それぞれそれが入っているかどうかを聞くことは同じである。
しかしこの場合は、1 枚目のカードに入っている、と言われたら、 それを表のまま 4 枚目のカードに重ねて載せる。 これは客には見えないように、机の上に重ねて置くとか、 手で持つ場合は手前に向けて重ねるとよいだろう。 そして入ってないと言われた場合は、 1 枚目のカードを左右ひっくり返して裏にして 4 枚目に重ねる。
2 枚目のカードにも同じことを行い、 1 枚目のカードの上に表、または裏にして重ねる。
3 枚目のカードは、入ってる場合は同じであるが、 入ってない場合は左右をひっくり返すのではなく、 上下をひっくり返して裏にして、2 枚目のカードに重ねる。
そうすると、重ねた 3 枚のカードの穴から、 4 枚目のカードの数字が一つだけ見えていて、 実はそれが客が覚えた数字となる、ということになっている。
例えば客が覚えた数字が 24 である場合は、 1 枚目のカードには入っているので、表にして重ねると、 以下のように穴から 4 つの数字が顔を出す:
これは準備でやったように、1 枚目のカードに書いてある数字と同じである。
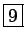
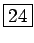
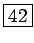
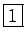
24 は 2 枚目にもあるから、これを表にして重ねると、 4 枚目のカードの数字は以下の 2 つだけが見えることになる。
これは、1 枚目と 2 枚目に共通に含まれる数字を意味する。
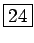
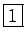
3 枚目には 24 は含まれないので、 上下をひっくり返して裏にして重ねると、穴は上にくるので、 結局右上の 24 のみが出てきて、それが元の数字となるわけである。
この方法も、 原理はほぼ 3 節に述べたものと同じである。 この 8 つの場所というのは、左上角が 0 で、 あとは右に順に 1, 2, 3, そして下の段に 4, 5, 6, 7 という数字が (内幕側に) 並んでいると見ていることになっている:
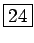
よってカードに開けた穴は、1 枚目のものが 1,3,5,7 に、 2 枚目のものが 2,3,6,7 に、 3 枚目のものが 4,5,6,7 に対応するので、 これは丁度 (1) を意味している。
0 1 2 3 4 5 6 7
しかも、1 枚目を左右逆にして裏返すと、 丁度穴の位置が 1,3,5,7 以外の位置 (0,2,4,6) にくるので、 そのカードに含まれない場合にそれ以外の数を残すことになっている。
2 枚目も同様であるが、 3 枚目は左右にひっくり返しても同じ位置に穴が来てしまうので、 上下にひっくり返すことで丁度穴が反転される。
これだと足し算をする必要もなくだいぶ楽であるが、 4 x 2 マスの 7 箇所のものでやるよりも、 4 x 4 マスの 15 箇所のカード 4 枚でやる方が効果は上がるだろう。
しかしこの場合も、やはり穴の位置が綺麗に並んでいることと、 3 枚目だけ上下にひっくり返すという点が少し問題だろうと思われるので、 今度はそれを解消することを考えてみる。
竹野茂治@新潟工科大学