4 漸化式
今度は、(1)-(5) を数列の漸化式とみて、
その数列の一般の式を求めることを考えてみることにする。
つまり、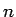 世代目の割合を、
世代目の割合を、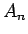 ,
, 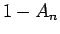 ,
, 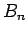 ,
, 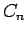 ,
, 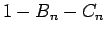 としてその漸化式を立てると、
(1)-(5) により、次が成り立つ。
としてその漸化式を立てると、
(1)-(5) により、次が成り立つ。
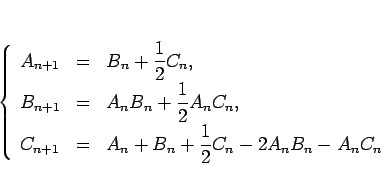 |
(6) |
もし、この右辺が 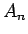 ,
, 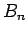 ,
, 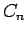 の一次式であれば、
の一次式であれば、
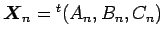 とすることで、係数行列
とすることで、係数行列 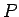 によって
によって
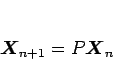
と書けるので、
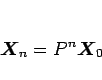
となり、線形代数の知識を用いれば、
この行列 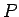 の固有値を求めることで
の固有値を求めることで
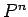 の成分を
の成分を 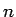 の式で表すことができ、
それにより
の式で表すことができ、
それにより
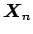 を、
そして
を、
そして 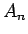 ,
, 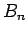 ,
, 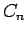 を
を 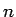 の式で表すことが可能となる。
の式で表すことが可能となる。
しかし、(6) の右辺は
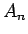 ,
, 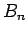 ,
, 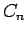 の 2 次式で非線形なので、
一般にはこのようなことは行えず、
の 2 次式で非線形なので、
一般にはこのようなことは行えず、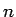 の式で表すことは難しい。
ただし、この漸化式 (6) の場合は、
これが特殊な形をしているので、
そこに着目してそれを求めることができる。
の式で表すことは難しい。
ただし、この漸化式 (6) の場合は、
これが特殊な形をしているので、
そこに着目してそれを求めることができる。
(6) の右辺には、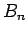 ,
, 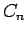 が、いずれも
が、いずれも
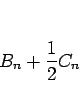
の形で入っているので、
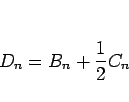 |
(7) |
とすると、(6) は、
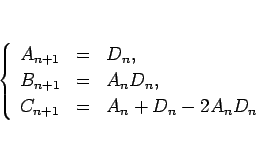 |
(8) |
と書け、これにより、
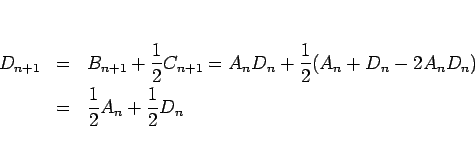
となり、よって、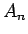 と
と 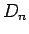 について
について
![\begin{displaymath}
\left\{\begin{array}{lll}
A_{n+1} & = & D_n,\\ [.5zh]
D_{...
...\displaystyle \frac{1}{2}A_n+\frac{1}{2}D_n
\end{array}\right.\end{displaymath}](img76.gif) |
(9) |
という漸化式を導くことができる。
この (9) の右辺は、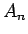 ,
, 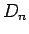 の 1 次式なので、
前の方針に従って、
の 1 次式なので、
前の方針に従って、
![\begin{displaymath}
\left[\begin{array}{c}A_{n+1}\\ D_{n+1}\end{array}\right]
...
...rray}\right]
\left[\begin{array}{c}A_n\\ D_n\end{array}\right]\end{displaymath}](img77.gif) |
(10) |
から 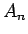 ,
, 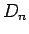 を求めることができる。
ただ、ここでは 2 本の方程式なので、行列を用いずに、
より素朴な方法 (特性方程式法) により
を求めることができる。
ただ、ここでは 2 本の方程式なので、行列を用いずに、
より素朴な方法 (特性方程式法) により 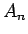 ,
, 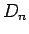 を求めてみる。
を求めてみる。
(9) の 1 本目から 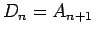 であり、
よって
であり、
よって
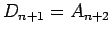 であるから、
これらを (9) の 2 本目に代入すれば
であるから、
これらを (9) の 2 本目に代入すれば
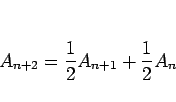 |
(11) |
という 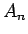 に対する 3 項漸化式が得られる。
に対する 3 項漸化式が得られる。
なお、この式 (11) は、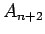 が、
その前の 2 つの項
が、
その前の 2 つの項 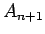 ,
, 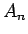 の平均であることも意味しているので、
これにより、他の数列を使わなくても
の平均であることも意味しているので、
これにより、他の数列を使わなくても 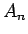 を単独で
容易に順次計算できることになる。
を単独で
容易に順次計算できることになる。
一般に、3 項漸化式
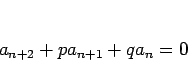 |
(12) |
に対して、2 次方程式
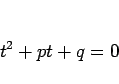 |
(13) |
を (12) の 特性方程式 という。
この特性方程式の解が
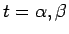 であるとき、
3 項漸化式 (12) は、
であるとき、
3 項漸化式 (12) は、
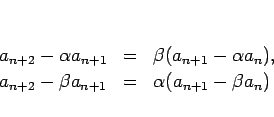
の形に変形できることが、
2 次方程式の解と係数の関係によって容易にわかる。
この 3 項漸化式 (11) の場合は、特性方程式は
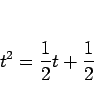
であるが、これを解くと
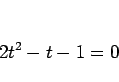
より、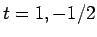 と求まる。(11) は、
と求まる。(11) は、
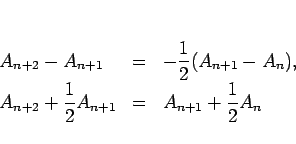
の 2 通りの形に変形できることになる。
これにより、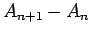 と
と 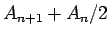 は、
それぞれ公比が
は、
それぞれ公比が 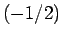 , 1 である等比数列であることになり、よって、
, 1 である等比数列であることになり、よって、
となるので、(15) から (14) を引いて
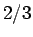 倍すれば、
倍すれば、
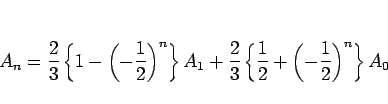
となり、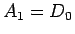 より、結局
より、結局
が得られる。
 は、
は、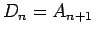 であるから、(16) より、
であるから、(16) より、
となる。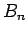 ,
, 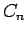 は、(8),
(7) により、
は、(8),
(7) により、
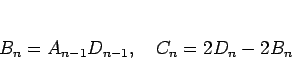 |
(18) |
より求めることができる (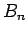 ,
, 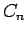 の一般形は複雑なので省略)。
の一般形は複雑なので省略)。
竹野茂治@新潟工科大学
2007年9月4日
![]() ,
, ![]() ,
, ![]() の 2 次式で非線形なので、
一般にはこのようなことは行えず、
の 2 次式で非線形なので、
一般にはこのようなことは行えず、![]() の式で表すことは難しい。
ただし、この漸化式 (6) の場合は、
これが特殊な形をしているので、
そこに着目してそれを求めることができる。
の式で表すことは難しい。
ただし、この漸化式 (6) の場合は、
これが特殊な形をしているので、
そこに着目してそれを求めることができる。
![]() ,
, ![]() が、いずれも
が、いずれも
![]() ,
, ![]() の 1 次式なので、
前の方針に従って、
の 1 次式なので、
前の方針に従って、
![]() であり、
よって
であり、
よって
![]() であるから、
これらを (9) の 2 本目に代入すれば
であるから、
これらを (9) の 2 本目に代入すれば
![]() が、
その前の 2 つの項
が、
その前の 2 つの項 ![]() ,
, ![]() の平均であることも意味しているので、
これにより、他の数列を使わなくても
の平均であることも意味しているので、
これにより、他の数列を使わなくても ![]() を単独で
容易に順次計算できることになる。
を単独で
容易に順次計算できることになる。
![]() は、
は、![]() であるから、(16) より、
であるから、(16) より、