2 物理的な重心の定義
重心とは、質量を持った物体 (の集まり) に対して、
その 1 次モーメントがつり合う点を指す。
ここで、点 P に質量 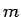 があるとき、
その質点の点 A に対する 1 次モーメント とは、
ベクトル
があるとき、
その質点の点 A に対する 1 次モーメント とは、
ベクトル
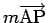 のことであるとする。
のことであるとする。
まず、「点」(質点系) に対する重心を考える。
3 次元空間内の 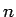 個の点
個の点
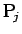 (
(
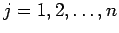 ) に質量
) に質量 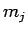 があるとき、その重心 G は
があるとき、その重心 G は
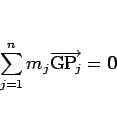 |
(1) |
が成り立つ点となる。
これら質点の総質量
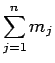 を
を 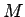 とすると、
(1) の左辺は
とすると、
(1) の左辺は
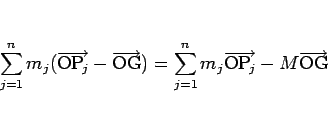
となるので、重心 G の位置ベクトルは
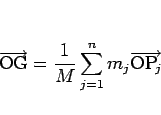 |
(2) |
と表すことができる。
特に、各点の質量 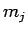 がすべて等しいときは
がすべて等しいときは
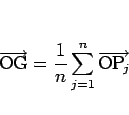 |
(3) |
の形となる。
次に、「線」に対する重心を考える。
例えば針金のように、3 次元空間内の質量を持つ曲線 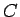 を考える。
を考える。
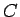 上の点を
上の点を 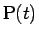 (
(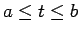 ) で表し、
) で表し、
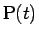 での針金の線密度、
すなわち単位長さ当たりの質量を
での針金の線密度、
すなわち単位長さ当たりの質量を
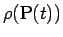 とする。
とする。
このとき、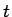 の範囲
の範囲 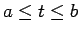 を
を 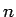 等分し、
この針金を細かく分割する:
等分し、
この針金を細かく分割する:
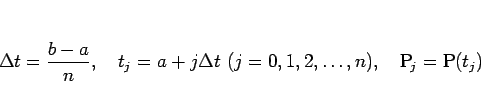
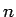 を十分大きくとれば、
各
を十分大きくとれば、
各 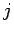 に対し
に対し
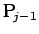 から
から
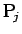 までの弧の長さ
までの弧の長さ 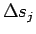 は十分小さく、それぞれの重心は
は十分小さく、それぞれの重心は
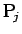 に近いので、
この針金の重心 G に対しては (1) より
に近いので、
この針金の重心 G に対しては (1) より
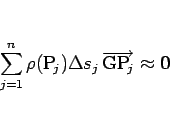
が成り立ち、この式で
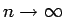 とすれば左辺は線積分に、
両辺の誤差は 0 に収束し、
重心 G の満たす条件式
とすれば左辺は線積分に、
両辺の誤差は 0 に収束し、
重心 G の満たす条件式
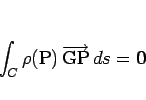 |
(4) |
が得られる。
ここで、針金の総質量
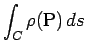 を
を 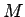 とすれば、
(2) と同様に G の位置ベクトルの表現式
とすれば、
(2) と同様に G の位置ベクトルの表現式
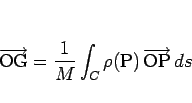 |
(5) |
が得られ、
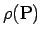 が一定ならば、
が一定ならば、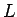 を曲線
を曲線 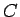 の長さとして
の長さとして
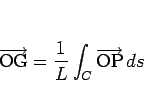 |
(6) |
が得られる。
同様に、「面」としての重心は、
曲面 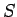 の点 P での面密度 (単位面積当たりの質量) を
の点 P での面密度 (単位面積当たりの質量) を
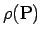 とすれば、重心 G の条件は面積分により、
とすれば、重心 G の条件は面積分により、
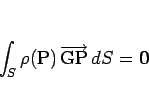 |
(7) |
と表わされ、よって総質量
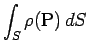 を
を 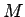 とすれば
とすれば
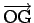 は
は
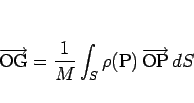 |
(8) |
と表され、
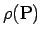 が一定ならば、
が一定ならば、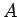 を曲面
を曲面 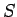 の面積として
の面積として
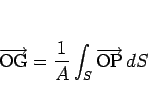 |
(9) |
が得られる。
また、「立体」としての重心は、
立体 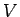 の点 P での体積密度 (単位体積当たりの質量) を
の点 P での体積密度 (単位体積当たりの質量) を
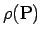 とすれば、重心 G の条件は体積分により
とすれば、重心 G の条件は体積分により
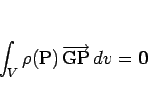 |
(10) |
と表わされ、よって総質量
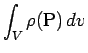 を
を 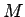 とすれば
とすれば
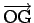 は
は
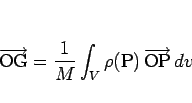 |
(11) |
と表され、
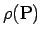 が一定ならば、
が一定ならば、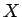 を曲面
を曲面 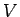 の体積として
の体積として
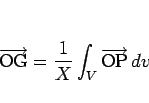 |
(12) |
が得られる。
(1), (4), (7), (10) からわかるが、
いずれの場合も重心では、
任意の重力方向
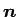 (
(
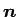 は単位ベクトル) に対して重心への回転モーメント
は単位ベクトル) に対して重心への回転モーメント
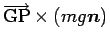 の和や積分が
の和や積分が
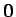 となるので、この点で物体を支えればそれは静止する。
となるので、この点で物体を支えればそれは静止する。
また、(2), (5), (8), (11) からわかるが、
任意の点 A に対するこれらの物体による 1 次モーメントは、
いずれも重心に総質量が集中していると考えた場合の 1 次モーメント
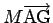 に等しくなる。
例えば、質点系の場合は、(2) より
に等しくなる。
例えば、質点系の場合は、(2) より
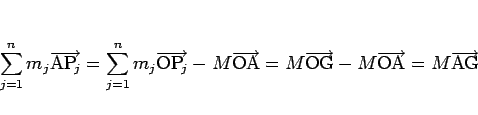
となるからである。線、面、立体の場合も同様である。
竹野茂治@新潟工科大学
2010年4月23日
![]() 個の点
個の点
![]() (
(
![]() ) に質量
) に質量 ![]() があるとき、その重心 G は
があるとき、その重心 G は
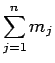 を
を ![]() を考える。
を考える。
![]() 上の点を
上の点を ![]() (
(![]() ) で表し、
) で表し、
![]() での針金の線密度、
すなわち単位長さ当たりの質量を
での針金の線密度、
すなわち単位長さ当たりの質量を
![]() とする。
とする。
![]() の範囲
の範囲 ![]() を
を ![]() 等分し、
この針金を細かく分割する:
等分し、
この針金を細かく分割する:
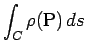 を
を ![]() の点 P での面密度 (単位面積当たりの質量) を
の点 P での面密度 (単位面積当たりの質量) を
![]() とすれば、重心 G の条件は面積分により、
とすれば、重心 G の条件は面積分により、
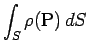 を
を 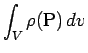 を
を ![]() (
(
![]() は単位ベクトル) に対して重心への回転モーメント
は単位ベクトル) に対して重心への回転モーメント
![]() の和や積分が
の和や積分が
![]() となるので、この点で物体を支えればそれは静止する。
となるので、この点で物体を支えればそれは静止する。
![]() に等しくなる。
例えば、質点系の場合は、(2) より
に等しくなる。
例えば、質点系の場合は、(2) より