2 内サイクロイド
内サイクロイドは、半径 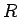 の円内に、半径
の円内に、半径 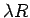 (
(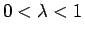 ) の
小円が内接しながらすべらずにころがるときの、小円の円周上の点が
描く軌跡である (図 1)。
最初に A
) の
小円が内接しながらすべらずにころがるときの、小円の円周上の点が
描く軌跡である (図 1)。
最初に A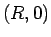 で接していた小円がころがって S
で接していた小円がころがって S
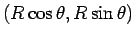 まで接点が進んだときの小円の中心を T、
元々 A にあった小円の円周上の点が回転した移動先、
すなわち内サイクロイド上の点を U
まで接点が進んだときの小円の中心を T、
元々 A にあった小円の円周上の点が回転した移動先、
すなわち内サイクロイド上の点を U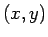 とし、
その小円の接点に対する回転角を
とし、
その小円の接点に対する回転角を 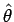 とすると、
とすると、
となる。大円の弧 AS は 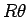 に等しいが、小円はすべらずにころがるので、
これは小円の弧 SU
に等しいが、小円はすべらずにころがるので、
これは小円の弧 SU
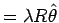 に等しくなり、
に等しくなり、
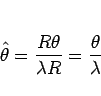 |
(8) |
となる。よって
となり、結局内サイクロイドは以下のように媒介変数表示される。
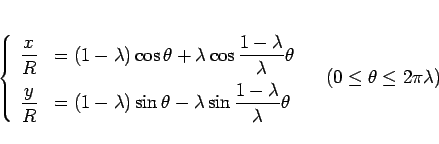 |
(9) |
なお、U が再び大円に接するのは
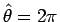 のときだから、
滑らかな内サイクロイドを与える
のときだから、
滑らかな内サイクロイドを与える 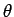 の範囲は (8) より
の範囲は (8) より
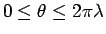 となる。
これをいくつかの
となる。
これをいくつかの 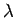 に対してグラフにすると図 2 の
ようになる。
に対してグラフにすると図 2 の
ようになる。
図 2:
内サイクロイドのグラフ
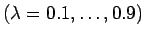
|
|
このグラフでは、
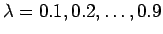 の内サイクロイドを
描いているが、
の内サイクロイドを
描いているが、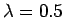 のときは
のときは 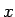 軸の一部分である直径に一致し、
軸の一部分である直径に一致し、
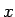 軸より下の部分は
軸より下の部分は 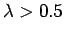 の場合に対応する。
の場合に対応する。
なお、この内サイクロイドのグラフは、以下の図 3 の
ように (9) を
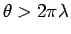 の方にも延長して
星形に描いたりするグラフも良く見られる。
の方にも延長して
星形に描いたりするグラフも良く見られる。
図 3:
星形に延長した内サイクロイド
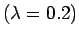
|
|
この方法を応用した幾何学文様を描くスピログラフという道具もあるが、
スピログラフは厳密には小円の円周上の点の軌跡ではなく、
小円板内部の点の軌跡であり、それは内サイクロイドではなく、
尖りのないトロコイドという曲線になる。
竹野茂治@新潟工科大学
2017年8月2日
![]() の方にも延長して
星形に描いたりするグラフも良く見られる。
の方にも延長して
星形に描いたりするグラフも良く見られる。