5 サイクロイド
通常サイクロイド曲線は、半径 1 の車輪で作られるものをさす。
半径 1 の車輪を、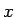 軸の上を右に転がしていくとき、
その車輪上の点の移動する軌跡がサイクロイドである (図 2)。
回転角を
軸の上を右に転がしていくとき、
その車輪上の点の移動する軌跡がサイクロイドである (図 2)。
回転角を 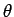 とすると、OQ は弧 PQ の長さに等しいので、
Q(
とすると、OQ は弧 PQ の長さに等しいので、
Q(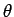 , 0) で、よって P(
, 0) で、よって P(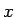 ,
,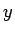 ) の座標は、
) の座標は、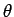 を用いて、
を用いて、
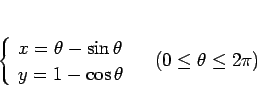 |
(24) |
と表される。
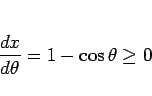
からもわかるが、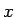 は
は 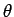 に関して
に関して
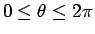 で
単調で、
で
単調で、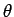 と
と 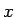 は 1 対 1 に対応する。
そして
は 1 対 1 に対応する。
そして
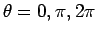 はそれぞれ
はそれぞれ
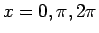 に対応する。
に対応する。
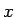 と
と 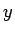 の対応は、
の対応は、
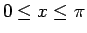 では
では 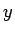 は 0 から 2 まで単調に増加し、
そこから対称に
は 0 から 2 まで単調に増加し、
そこから対称に
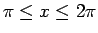 では
では 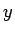 は単調に減少して 0 になる (図 3)。
なお、このグラフは一見楕円に似ているが、
図 3 に見られるように楕円とは多少ずれが
ある1。
は単調に減少して 0 になる (図 3)。
なお、このグラフは一見楕円に似ているが、
図 3 に見られるように楕円とは多少ずれが
ある1。
この
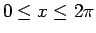 上で (24) により
定義されるサイクロイド関数を、今後
上で (24) により
定義されるサイクロイド関数を、今後
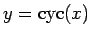 と書くことにする。
この関数の導関数は、
と書くことにする。
この関数の導関数は、
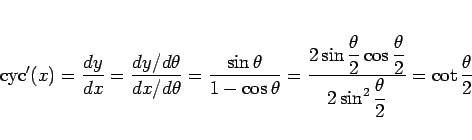 |
(25) |
となるので、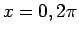 (
(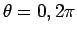 ) に特異性を持ち、
) に特異性を持ち、
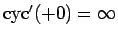 ,
,
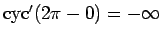 であることに注意する。
であることに注意する。
さて、4 節で (22) の積分により、
サイクロイド関数
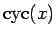 を
を 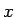 ,
, 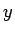 両方向に等倍に拡大 (縮小) した
関数を上下逆さにしたもの
両方向に等倍に拡大 (縮小) した
関数を上下逆さにしたもの
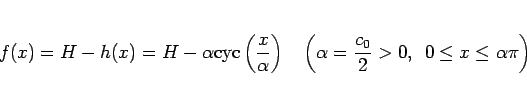 |
(26) |
が、(19) を満たす関数であることを見たが、
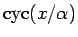 自身は
自身は
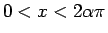 で滑らかな関数になっている。
まず、(26) がそこまで含めて
方程式 (20) を満たすか調べてみる。
で滑らかな関数になっている。
まず、(26) がそこまで含めて
方程式 (20) を満たすか調べてみる。
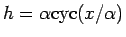 は
は
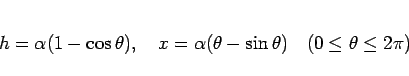
で表され、よって (25) より
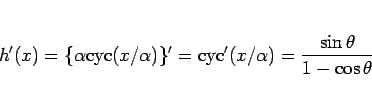
となるので、(20) の左辺に代入すると、
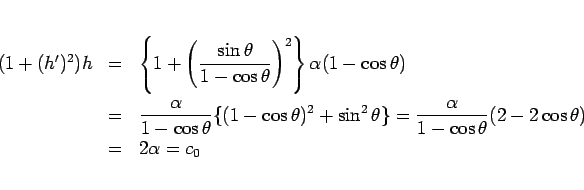
となり、
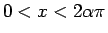 で (20) を満たす
ことがわかる。
で (20) を満たす
ことがわかる。
しかし、
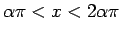 では
では 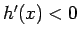 なので、
この
なので、
この
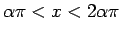 の部分は (21) の
マイナス符号の式に対応する。
すなわち (21) から (22) を
導くところでは、
の部分は (21) の
マイナス符号の式に対応する。
すなわち (21) から (22) を
導くところでは、
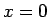 の近くでは
の近くでは 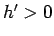 だからプラス符号の式を積分するが、
あるところで
だからプラス符号の式を積分するが、
あるところで 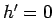 となり、
そこから先はマイナス符号の式を積分することで、
左右対称な形で
となり、
そこから先はマイナス符号の式を積分することで、
左右対称な形で 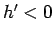 でつながるということになる。
でつながるということになる。
このように 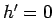 のところで抜けおちる (20) の
解は他にもあり、(20) は
のところで抜けおちる (20) の
解は他にもあり、(20) は
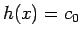
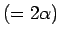 という特異解を持つ。
よって、
という特異解を持つ。
よって、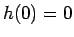 となる解としては、
上に見た
となる解としては、
上に見た
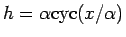 以外に、
それを
以外に、
それを 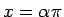 のところで切り離し、定数
のところで切り離し、定数 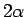 でそれらを
つないだもの (図 4)
でそれらを
つないだもの (図 4)
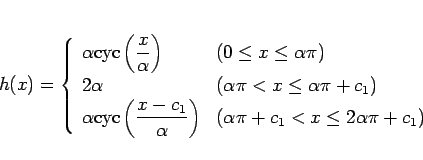 |
(27) |
なども解になっていて、よって微分方程式 (20) の
 の初期値問題の解の一意性は成り立たない。
の初期値問題の解の一意性は成り立たない。
なお、サイクロイド関数の 2 階微分は、
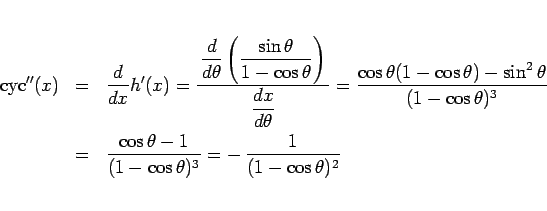
なので
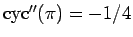 となり、
定数をサイクロイドの間に入れた (27) の形の解は、
となり、
定数をサイクロイドの間に入れた (27) の形の解は、
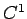 級だが
級だが 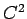 級ではないことがわかる。
ただし、方程式 (20) 自体は 1 階の方程式だから、
(27) は
級ではないことがわかる。
ただし、方程式 (20) 自体は 1 階の方程式だから、
(27) は 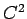 級でなくても
一応正しく (20) を満たしてはいる。
級でなくても
一応正しく (20) を満たしてはいる。
竹野茂治@新潟工科大学
2016年1月8日
![]() 上で (24) により
定義されるサイクロイド関数を、今後
上で (24) により
定義されるサイクロイド関数を、今後
![]() と書くことにする。
この関数の導関数は、
と書くことにする。
この関数の導関数は、
![]() を
を ![]() ,
, ![]() 両方向に等倍に拡大 (縮小) した
関数を上下逆さにしたもの
両方向に等倍に拡大 (縮小) した
関数を上下逆さにしたもの
![]() は
は
![]() では
では ![]() なので、
この
なので、
この
![]() の部分は (21) の
マイナス符号の式に対応する。
すなわち (21) から (22) を
導くところでは、
の部分は (21) の
マイナス符号の式に対応する。
すなわち (21) から (22) を
導くところでは、
![]() の近くでは
の近くでは ![]() だからプラス符号の式を積分するが、
あるところで
だからプラス符号の式を積分するが、
あるところで ![]() となり、
そこから先はマイナス符号の式を積分することで、
左右対称な形で
となり、
そこから先はマイナス符号の式を積分することで、
左右対称な形で ![]() でつながるということになる。
でつながるということになる。
![]() のところで抜けおちる (20) の
解は他にもあり、(20) は
のところで抜けおちる (20) の
解は他にもあり、(20) は
![]()
![]() という特異解を持つ。
よって、
という特異解を持つ。
よって、![]() となる解としては、
上に見た
となる解としては、
上に見た
![]() 以外に、
それを
以外に、
それを ![]() のところで切り離し、定数
のところで切り離し、定数 ![]() でそれらを
つないだもの (図 4)
でそれらを
つないだもの (図 4)