4 連続曲線の交点
前節と同様の方法で、2 次元のブラウアーの不動点定理を用いて、
問題 2 を考えることにする。
問題 2 の
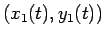 で表される曲線を
で表される曲線を 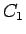 、
、
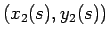 で表される曲線を
で表される曲線を 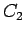 と書くこととし、
2 変数関数
と書くこととし、
2 変数関数 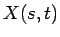 ,
, 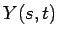 を
を
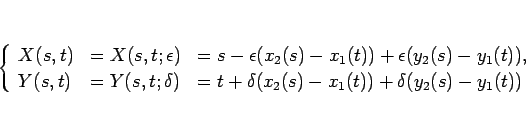 |
(6) |
と定める (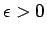 ,
, 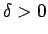 ,
, ![$s,t\in [0,1]$](img87.gif) )。
前節と同様に、
)。
前節と同様に、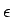 ,
, 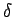 を十分小さく取れば、
すべての
を十分小さく取れば、
すべての ![$s,t\in [0,1]$](img87.gif) に対して、
に対して、
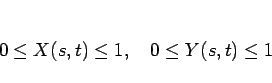 |
(7) |
となることを示すことが目標となる。
もし、これが言えれば、2 次元のブラウアーの不動点定理を適用することで、
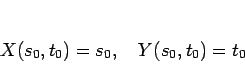
となる
![$s_0,t_0\in [0,1]$](img91.gif) が存在し、
そしてこれは (6) より明らかに
が存在し、
そしてこれは (6) より明らかに
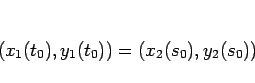
を意味するので、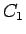 と
と 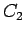 の交点の存在が示されることになる。
の交点の存在が示されることになる。
なお、今後は (7) を示すわけであるが、
そのために 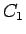 と
と 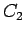 の交点が存在しない、と仮定してよいことに注意する。
つまり、背理法で考え、
の交点が存在しない、と仮定してよいことに注意する。
つまり、背理法で考え、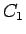 と
と 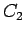 の交点が存在しないと仮定するとき、
(7) が十分小さい
の交点が存在しないと仮定するとき、
(7) が十分小さい 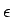 ,
, 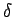 に対して言えてくれれば、
上の論法でブラウアーの定理により交点の存在が言えてしまうので矛盾、
となるからである。
に対して言えてくれれば、
上の論法でブラウアーの定理により交点の存在が言えてしまうので矛盾、
となるからである。
前節と同じ論法で、もし
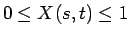 が言えないとすると、
が言えないとすると、
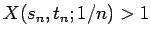 か、
か、
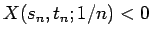 となる点列
となる点列 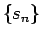 ,
, 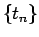 が取れることになるが、
まず
が取れることになるが、
まず
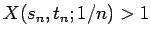 となる
となる 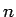 が無限にある場合を考えると、
が無限にある場合を考えると、
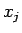 ,
, 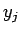 は有界であるから、
は有界であるから、
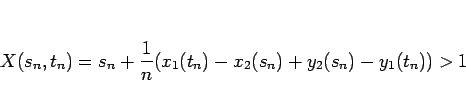 |
(8) |
より、
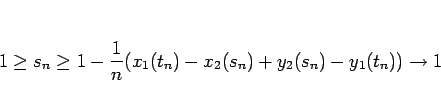
から
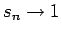 が言える。一方、(8) より、
が言える。一方、(8) より、
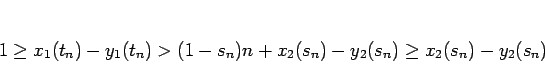
であり、
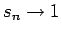 と (2) より
と (2) より
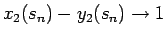 となるので、
よって
となるので、
よって
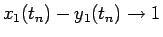 となる。
となる。
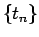 は有界無限点列であるから集積点を持ち、
その集積点を
は有界無限点列であるから集積点を持ち、
その集積点を ![$t_0\in[0,1]$](img105.gif) とすれば、
とすれば、
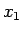 ,
, 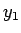 は連続であるから
は連続であるから
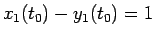 となることが言える。
これは、
となることが言える。
これは、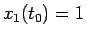 ,
, 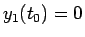 しかありえないが、
この点
しかありえないが、
この点
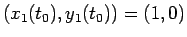 は
は 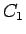 上の点で
かつ
上の点で
かつ 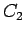 の終点であるから、両者の共有点となる。
よって交点がないとしているので矛盾となる。
の終点であるから、両者の共有点となる。
よって交点がないとしているので矛盾となる。
他の 3 通り (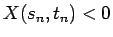 ,
, 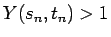 ,
, 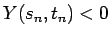 ) の場合も、
同様の論法でいずれも (2) と
) の場合も、
同様の論法でいずれも (2) と 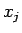 ,
, 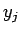 の連続性から
矛盾が導きだせるので、
結局 (7) とできることが言え、
そこから連続曲線の交点の存在を示せることになる。
の連続性から
矛盾が導きだせるので、
結局 (7) とできることが言え、
そこから連続曲線の交点の存在を示せることになる。
竹野茂治@新潟工科大学
2012年4月16日
![]() と
と ![]() の交点が存在しない、と仮定してよいことに注意する。
つまり、背理法で考え、
の交点が存在しない、と仮定してよいことに注意する。
つまり、背理法で考え、![]() と
と ![]() の交点が存在しないと仮定するとき、
(7) が十分小さい
の交点が存在しないと仮定するとき、
(7) が十分小さい ![]() ,
, ![]() に対して言えてくれれば、
上の論法でブラウアーの定理により交点の存在が言えてしまうので矛盾、
となるからである。
に対して言えてくれれば、
上の論法でブラウアーの定理により交点の存在が言えてしまうので矛盾、
となるからである。
![]() が言えないとすると、
が言えないとすると、
![]() か、
か、
![]() となる点列
となる点列 ![]() ,
, ![]() が取れることになるが、
まず
が取れることになるが、
まず
![]() となる
となる ![]() が無限にある場合を考えると、
が無限にある場合を考えると、
![]() ,
, ![]() は有界であるから、
は有界であるから、
![]() ,
, ![]() ,
, ![]() ) の場合も、
同様の論法でいずれも (2) と
) の場合も、
同様の論法でいずれも (2) と ![]() ,
, ![]() の連続性から
矛盾が導きだせるので、
結局 (7) とできることが言え、
そこから連続曲線の交点の存在を示せることになる。
の連続性から
矛盾が導きだせるので、
結局 (7) とできることが言え、
そこから連続曲線の交点の存在を示せることになる。