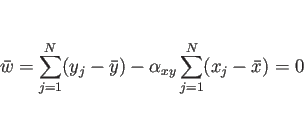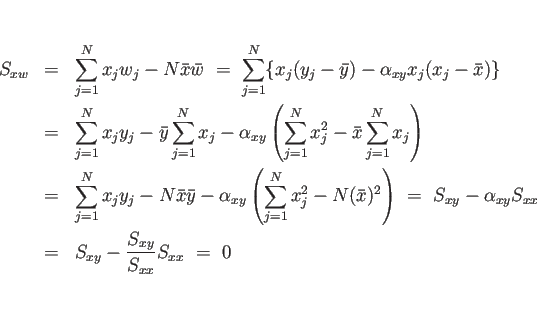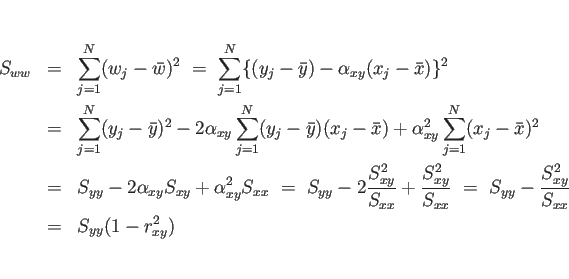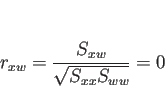4 伸びとの相関
本節で、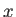 と伸びとの相関を調べてみる。まずは
と伸びとの相関を調べてみる。まずは 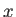 と
と 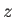 から。
から。
より、
となる。よって、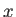 と
と 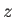 の相関係数
の相関係数 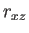 は
は
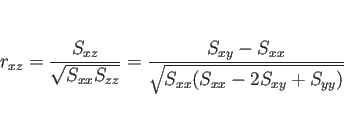 |
(11) |
となるので、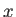 と
と 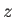 の相関は必ずしも 0 になるわけではなく、
相関が 0 になるのは
の相関は必ずしも 0 になるわけではなく、
相関が 0 になるのは 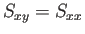 のとき、
すなわち
のとき、
すなわち 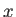 と
と 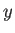 の回帰直線 (6) の傾き
の回帰直線 (6) の傾き 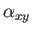 が 1 のとき、となる。
元々の回帰直線の傾きが 1 に近ければ
が 1 のとき、となる。
元々の回帰直線の傾きが 1 に近ければ 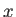 と
と 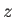 との相関は
小さくなるが、一般にはそうとも限らない。
との相関は
小さくなるが、一般にはそうとも限らない。
次は 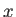 と
と 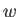 の相関を考える。
の相関を考える。
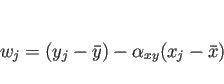 |
(12) |
より、
すなわち 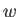 の平均は 0 となる。よって、
の平均は 0 となる。よって、
となり、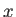 ,
, 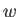 の積和は 0 となる。一応
の積和は 0 となる。一応 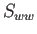 も計算してみると、
も計算してみると、
となるので、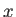 と
と 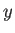 が完全に直線相関 (
が完全に直線相関 (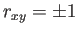 ) で
なければ
) で
なければ 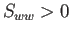 であり、
であり、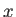 ,
, 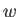 の相関は
の相関は
すなわち、相関は常に 0 であることがわかる。
竹野茂治@新潟工科大学
2019-06-05
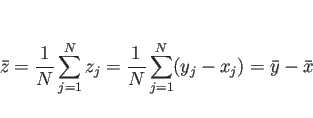
![]() と
と ![]() の相関を考える。
の相関を考える。