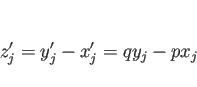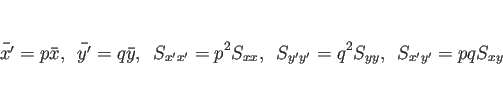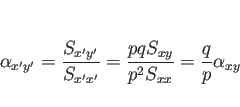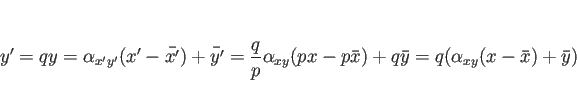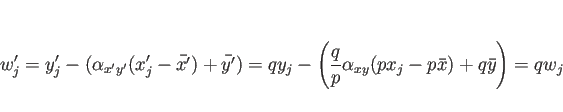3 伸び
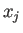 ,
, 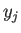 が 1 回目と 2 回目のテストの点数のように、
同種のデータである場合は、
その差
が 1 回目と 2 回目のテストの点数のように、
同種のデータである場合は、
その差 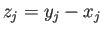 を値の「伸び」として考えることができる。
これが
を値の「伸び」として考えることができる。
これが 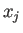 の値と相関があるのか、
すなわち
の値と相関があるのか、
すなわち 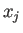 が大きいほど伸びは大きくなるのか、
または
が大きいほど伸びは大きくなるのか、
または 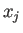 がむしろ小さい方が伸びは大きくなるのか、
などを調べたくなることもまた自然であろう。
がむしろ小さい方が伸びは大きくなるのか、
などを調べたくなることもまた自然であろう。
伸びとしては、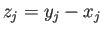 以外に、
以外に、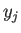 と
と 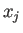 での回帰直線の値との差
での回帰直線の値との差
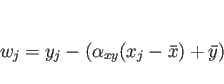 |
(8) |
を考えることもできる。
回帰直線の値は、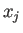 に対する平均的な
に対する平均的な 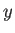 の値、
期待される
の値、
期待される 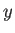 の値を意味し、
の値を意味し、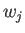 はそれとの差であり、
よって全体のデータから決まる相対的な伸びを意味することになる。
はそれとの差であり、
よって全体のデータから決まる相対的な伸びを意味することになる。
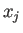 と
と 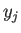 の単位が違う場合には
の単位が違う場合には 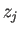 のような差よりも
むしろ
のような差よりも
むしろ 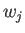 の方が伸びとしては適切だろうし、
また
の方が伸びとしては適切だろうし、
また 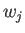 はスケール変換にも強い。
例えば、
はスケール変換にも強い。
例えば、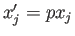 ,
, 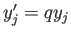 とすると、
とすると、
より 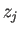 の分布とはかなり変わってしまう可能性があるが、
の分布とはかなり変わってしまう可能性があるが、
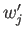 の方は、
の方は、
より、
となり、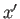 ,
, 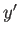 の回帰直線は、
の回帰直線は、
となり、実質的に (6) と同じものになり、
となって、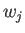 の分布を
の分布を 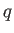 倍しただけなので、
実質的に分布は変わらず、スケール変換に影響されないことがわかる。
倍しただけなので、
実質的に分布は変わらず、スケール変換に影響されないことがわかる。
竹野茂治@新潟工科大学
2019-06-05
![]() 以外に、
以外に、![]() と
と ![]() での回帰直線の値との差
での回帰直線の値との差
![]() と
と ![]() の単位が違う場合には
の単位が違う場合には ![]() のような差よりも
むしろ
のような差よりも
むしろ ![]() の方が伸びとしては適切だろうし、
また
の方が伸びとしては適切だろうし、
また ![]() はスケール変換にも強い。
例えば、
はスケール変換にも強い。
例えば、![]() ,
, ![]() とすると、
とすると、