a 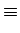 b(mod x)
b(mod x)
閏年の場合は、平年に比べて 1, 2 月は一つずつ減る (戻る) と考えれば、 このうち平年の方だけ考えればよい。 この各月の先頭の曜日の数字は、 月同士の曜日のずれがどれくらいであるかも示していることになるので、 この平年の表をなんらかの形で覚えてしまえば、 各月のカレンダーの曜日のずれがすぐにわかることになる。
例えば、5 月 10 日が火曜であるとき、9 月 23 日が何曜日であるかを考えてみる。
5 月 1 日と 9 月 1 日は、上の表により 2 - 5 = (- 3) 曜日ずれている。 よって、5 月 10 日が火曜 (=2) であれば、 9 月 10 日は 2 + (- 3) = - 1 なので、 9 月 23 日は -1 + (23 - 10) = 12 となり、 これを 7 で割った余りは 5、すなわち 金曜日ということになる。
このように、今日の日付の曜日を基準にし、 知りたい日付の月同士のずれを上の表から求め、 日付のずれを加えて、7 で割った余りを考えれば 任意の日付の曜日が求められることになる。
この計算は、式で書けば以下のようになる:
| (9/23の曜日)-(5/10の曜日) | |||
| = | {(9/23の曜日) - (9/10の曜日)} + {(9/10の曜日) - (5/10の曜日)} | ||
| = | 13 + {(9/1の曜日) - (5/1の曜日)} = 13 + (2 - 5) = 10, | ||
(9/23の曜日) = (5/10の曜日) + 10 = 2 + 10 = 12 = 7 + 5 = (金曜日)
なお、数学では
と書くと、「a を x で割った余りと b を x で割った余りが 等しい」ことを示すので、上の計算の最後のところは、
ab(mod x)
のように書くことができる。
2 + 10 = 125(mod 7)
竹野茂治@新潟工科大学