4 余りの作る体
この余りについては、次のことが成り立つことが知られている
(いずれも容易に証明ができるので考えてみるとよいだろう)。
a 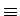 p
,
b
p
,
b 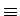 q(mod x)
のとき、
q(mod x)
のとき、
-
a + b
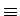 p + q(mod x)
p + q(mod x)
-
a - b
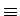 p - q(mod x)
p - q(mod x)
-
a x b
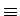 p x q(mod x)
p x q(mod x)
つまり、元の数字の和、差、積の余りは、
余りの和、差、積 (の余り) と同じである、ということになる。
曜日の数字は 0 から 6 まで進み、その次はまた 0 に戻る、
といった形で考えることになるが、
これは前に述べたように 7 で割った余りを考えることになる。
特に 7 のように素数で割った余りの数字にの場合は
割り算もできることが知られていて、このような余りの世界を
数学では 体 と呼んでいる。
7 の余りの積の表を表 6 に示すが、
表 6:
7 の余りの積の表
| x
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| 2 |
0 |
2 |
4 |
6 |
1 |
3 |
5 |
| 3 |
0 |
3 |
6 |
2 |
5 |
1 |
4 |
| 4 |
0 |
4 |
1 |
5 |
2 |
6 |
3 |
| 5 |
0 |
5 |
3 |
1 |
6 |
4 |
2 |
| 6 |
0 |
6 |
5 |
4 |
3 |
2 |
1 |
|
0 以外のどの列、どの行にも 0 から 6 のすべての数が現われることがわかる。
よって、a
が 0 でなければ
a x x 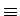 b(mod 7)
という x
が常に求まることになり、
この x
がこの 7 の余りの世界では b ÷ a
に相当することになる。
b(mod 7)
という x
が常に求まることになり、
この x
がこの 7 の余りの世界では b ÷ a
に相当することになる。
ただ、これが何に使えるかというとあまりいい例は思い浮かばないが、
無理矢理考えれば、次のような例がある。
問題:
あるプロ野球チームで、中 4 日 (5 日毎) に登板するピッチャーが
金曜日に登板したとすると、次に火曜日に登板するのは何日後のことか。
解答:
次の x
回目の登板は y = 5x
日後であるから、それが火曜日となるのは、
y + (金曜日) =
y + 5
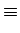
2(mod 7)
となるとき。よって、
| |
|
5x + 5 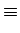 2(mod 7) 2(mod 7) |
|
| |
|
5x 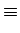 2 - 5 2 - 5 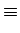 -3 -3 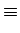 4(mod 7) 4(mod 7) |
|
| |
|
x 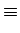 4 ÷ 5 4 ÷ 5 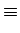 5(mod 7) (5 x 5 5(mod 7) (5 x 5 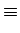 4(mod 7) より) 4(mod 7) より) |
|
となることが上の表 6 からわかる。
よって、
x = 5, 12,...
となり、最短で
y = 5 x 5 = 25
日後、となる。
竹野茂治@新潟工科大学
2007年12月20日
p , b
q(mod x) のとき、
2(mod 7)