回帰直線とは、データに直線的な相関がある場合に、 それを表す、最も妥当だと思われる直線を回帰直線という。 実際にはそれは以下のようにして求める。
まず、求める直線を ![]() とすると、データ
とすると、データ ![]() に直線相関がある場合は
に直線相関がある場合は
![]() となるので、
その誤差 (
となるので、
その誤差 (![]() ) の平方和を最も小さくする
) の平方和を最も小さくする ![]() ,
,![]() を取る、
という最小自乗法を用いる。
すなわち、
を取る、
という最小自乗法を用いる。
すなわち、
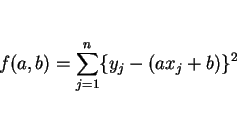
によって求めることにする。そのために次の性質を利用する。に関して最小になるところの中で、
に関して最小になるところを求める
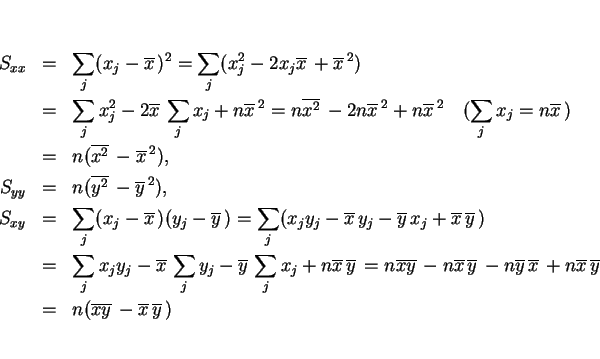
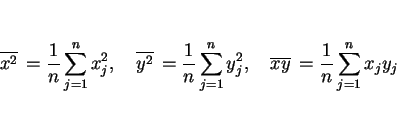
これらを用いると、![]() は以下のように展開される。
は以下のように展開される。
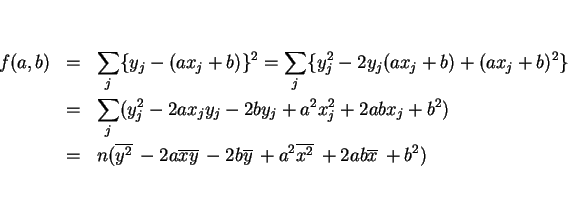
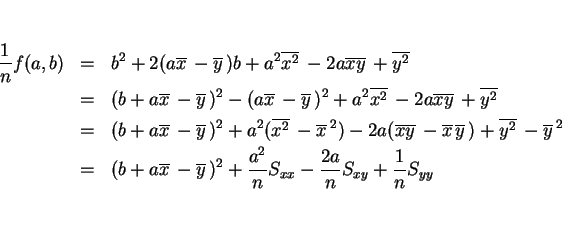
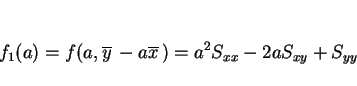
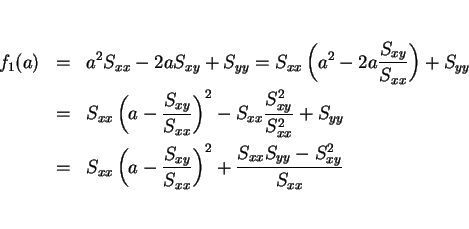
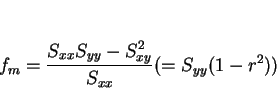
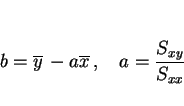
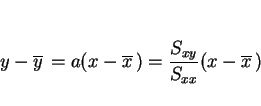
しかし、この式は明らかに ![]() ,
,![]() に関して対称ではない。
すなわち、「元のデータを
に関して対称ではない。
すなわち、「元のデータを ![]() とみて回帰直線を求めたもの」
と、「元のデータを
とみて回帰直線を求めたもの」
と、「元のデータを ![]() とみて回帰直線を求めたもの」は、
とみて回帰直線を求めたもの」は、
![]() に関して対称にはならない。
に関して対称にはならない。
例えば「![]() 身長、
身長、![]() 体重」のようなデータの場合、
どちらを横軸に取ってどちらを縦軸に取るか、
ということに余り意味はなさそうであるが、
上の非対称性は、そのどちらを横軸に取るかで回帰直線が本質的に変わってしまう、
ということを意味している。
体重」のようなデータの場合、
どちらを横軸に取ってどちらを縦軸に取るか、
ということに余り意味はなさそうであるが、
上の非対称性は、そのどちらを横軸に取るかで回帰直線が本質的に変わってしまう、
ということを意味している。
前の、相関係数の回転不変性に対する疑問と同様に、 これも直線相関を意味するものとして適当なのだろうかと疑問に思う。
そのような非対称性が起こるのは、もちろん、
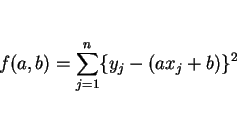
回帰直線に回転不変性や、![]() ,
,![]() の入れ替えに対する不変性を持たせるためには、
「データと直線の距離の平方和」を最小にする直線を考えれば良い。
これらの疑問をまとめると以下のようになる。
の入れ替えに対する不変性を持たせるためには、
「データと直線の距離の平方和」を最小にする直線を考えれば良い。
これらの疑問をまとめると以下のようになる。
問題 3 データ点と直線の距離の平方和を最小にする直線はどのような式になるか、 また、なぜ通常それを用いないのか