2 次元のデータ ![]() (
(
![]() ) があるとき、
これを
) があるとき、
これを ![]() 平面上に表示したときに (散布図)、
その点がある直線に近い、すなわち
平面上に表示したときに (散布図)、
その点がある直線に近い、すなわち ![]() と
と ![]() に
ほぼ一次的な関係があるときに相関があると言い、
そういう直線的な相関の見られないデータを相関がない、と言う。
に
ほぼ一次的な関係があるときに相関があると言い、
そういう直線的な相関の見られないデータを相関がない、と言う。
その相関を計る指標として相関係数がある。それは以下のように定義される。
まず、![]() の標本平均
の標本平均
![]() 、
、 ![]() の標本平均
の標本平均
![]() を
を
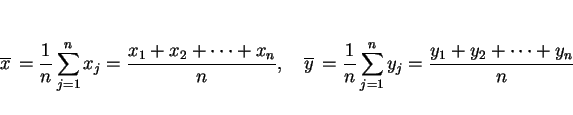
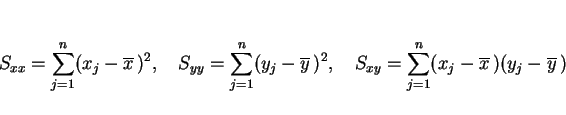
この ![]() であること、
そして
であること、
そして ![]() のときにデータが本当に一直線上にのるかを以下に説明する。
のときにデータが本当に一直線上にのるかを以下に説明する。
次元ベクトル
,
を
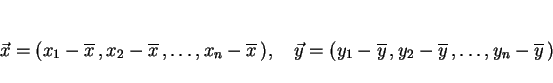
とすると、
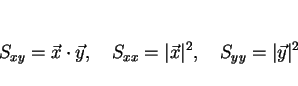
なので
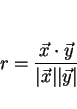
となる。厳密には、シュワルツの不等式から、
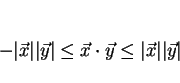
で、かつ等号成立はとなることが導かれ、 よって
で、
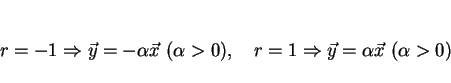
となることが言えるのであるが、 多少図形的なイメージで説明すると、高校の内積の定義にあるように
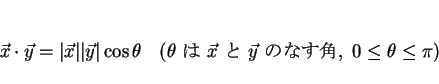
なのでとなり、 よってまず
がいえる。
となるのは
のときなので
と
が丁度逆向きのベクトルのとき、 すなわち
(
) となるが、 それを成分で見ると
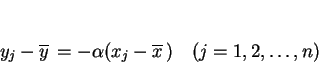
となり、これはが一つの直線
上にあることを意味することになる。
の場合も同様で、この場合は
となるので
と
が同じ向きのベクトルになり、 後は上の
を
に変えれば良い。
これにより、
![]() で、
で、![]() と
と ![]() は確かに直線相関なので、
そこから離れて 0 に近くなると確かに相関が小さいような気がする。
しかし、例えば
は確かに直線相関なので、
そこから離れて 0 に近くなると確かに相関が小さいような気がする。
しかし、例えば ![]() の場合に本当に相関がない、と言えるのだろうか。
上の式によれば
の場合に本当に相関がない、と言えるのだろうか。
上の式によれば ![]() の場合は
の場合は
![]() 、すなわち
、すなわち
![]() を意味するが、
それが「相関がない状態を意味している」と見なせるだろうか。
を意味するが、
それが「相関がない状態を意味している」と見なせるだろうか。
これが私が感じた最初の疑問である。
問題 1の状態は本当に (直線的な) 相関がない、といえるのだろうか
そして、![]() に含まれる式をみていてぼんやり思ったのは以下の疑問である。
に含まれる式をみていてぼんやり思ったのは以下の疑問である。
問題 2本来の値は、
全体を原点の周りに
だけ 回転しても変わらないだろうか