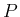 を、標本空間
を、標本空間
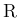 と、
分布関数
と、
分布関数 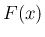 をセットにして、
をセットにして、
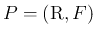 のように表す。
密度関数
のように表す。
密度関数 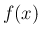 は
は 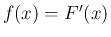 である。
である。
本稿では、連続確率分布 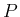 を、標本空間
を、標本空間
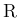 と、
分布関数
と、
分布関数 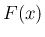 をセットにして、
をセットにして、
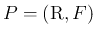 のように表す。
密度関数
のように表す。
密度関数 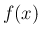 は
は 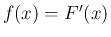 である。
である。
この場合も、独立な確率変数の和の分布で考える。
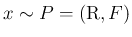 ,
,
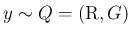 のとき、
のとき、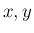 を独立として
考えた 2 次元確率変数
を独立として
考えた 2 次元確率変数 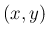 の分布関数は
の分布関数は
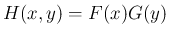 で、
密度関数は
で、
密度関数は
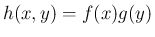 となる (
となる (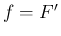 ,
, 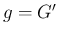 )。
よって、
)。
よって、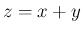 は、以下の
は、以下の 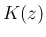 を分布関数とする確率変数となる。
を分布関数とする確率変数となる。
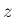 の密度関数は、これを
の密度関数は、これを 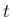 で微分した
となる。
逆に、
で微分した
となる。
逆に、
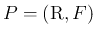 ,
,
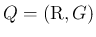 から (5) によって
作った
から (5) によって
作った 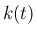 (
(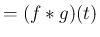 と書く) を密度関数とするような
連続確率分布を、
と書く) を密度関数とするような
連続確率分布を、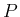 と
と 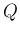 の「たたみこみ」と呼び、
の「たたみこみ」と呼び、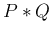 と書く。
と書く。
なお、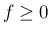 ,
, 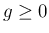 で
で
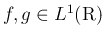 なので
なので 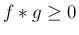 で、
で、
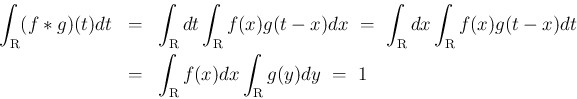
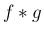 はある連続分布の密度関数となる。
はある連続分布の密度関数となる。
また、(4) より、
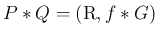 となるが、
これは次の命題 5 により
となるが、
これは次の命題 5 により
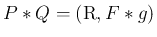 とも書ける。
とも書ける。
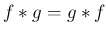
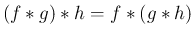
証明
1.
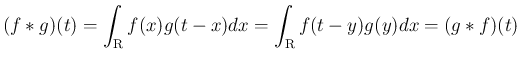
2.
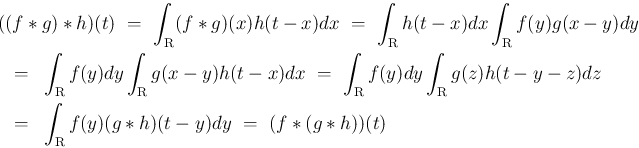
この命題 5 より、離散の場合同様、
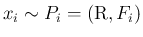 (
(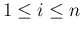 ) に対するたたみこみ
) に対するたたみこみ
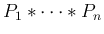 を考えることもできる。
を考えることもできる。
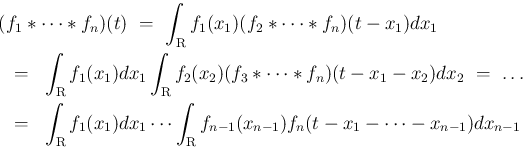
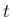 に関して
に関して 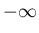 から
から 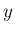 まで積分すると、
まで積分すると、
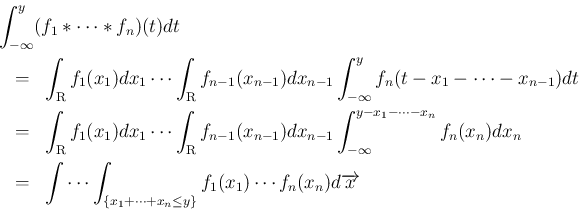
 を独立と見た場合の
を独立と見た場合の
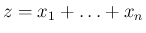 の分布関数にほかならない。よって、
の分布関数にほかならない。よって、
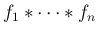 はその
はその 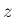 の密度関数となる。
の密度関数となる。
離散の場合と同様に、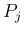 がすべて
がすべて
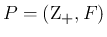 に等しい場合、
本稿では
に等しい場合、
本稿では 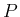 の
の 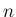 重のたたみこみを
重のたたみこみを
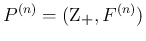 と書く。
と書く。
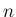 階導関数ではないので注意すること。
階導関数ではないので注意すること。
正規分布
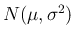 のたたみこみを計算する。
正規分布
のたたみこみを計算する。
正規分布
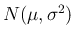 の密度関数を、
の密度関数を、
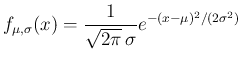
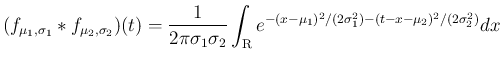
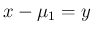 ,
,
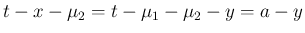 とすると、
とすると、
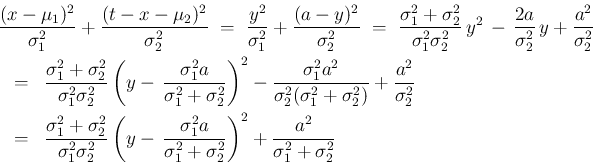
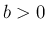 に対し、
に対し、
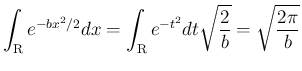
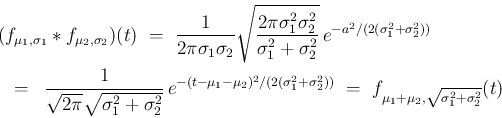
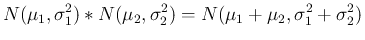
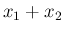 の分布であるから、
これは丁度 [2] の考察に対応する。
の分布であるから、
これは丁度 [2] の考察に対応する。
指数分布 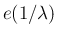 のたたみこみを計算する。
のたたみこみを計算する。
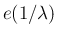 の密度関数
の密度関数 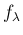 は (3) の
形なので、
は (3) の
形なので、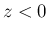 なら
なら
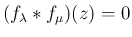 であり、
であり、
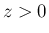 なら
なら
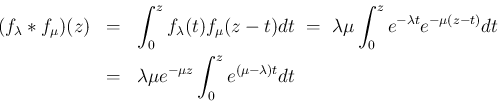
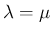 なら
なら
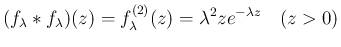
 なら
なら
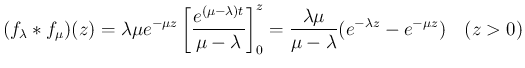
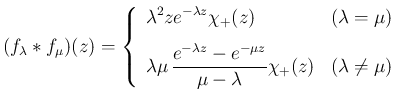
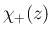 は、
は、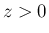 では 1、
では 1、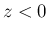 では 0 となる
関数とする。
これらはいずれも指数分布とは別の分布となる。
では 0 となる
関数とする。
これらはいずれも指数分布とは別の分布となる。
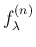 については、
については、
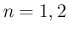 については上の結果より成立する。
については上の結果より成立する。
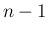 まで成り立つとすると (
まで成り立つとすると (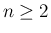 )、
)、 に対し、
に対し、
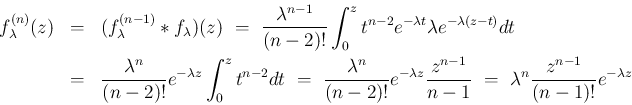
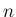 でも成立する。
ちなみに、
でも成立する。
ちなみに、
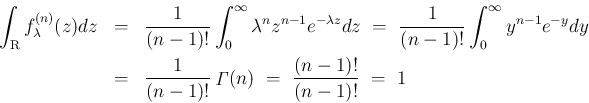
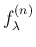 が確かにある分布の密度関数であることがわかるが、
これを密度関数として持つ分布はガンマ分布
が確かにある分布の密度関数であることがわかるが、
これを密度関数として持つ分布はガンマ分布
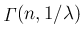 と呼ばれる。
よって、
と呼ばれる。
よって、
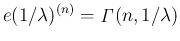 となる。
となる。
竹野茂治@新潟工科大学