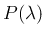
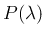 の「裏」が
指数分布
の「裏」が
指数分布 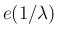 となることを考える。
指数分布
となることを考える。
指数分布 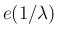 とは、
を分布関数とするような連続確率分布である。密度関数
とは、
を分布関数とするような連続確率分布である。密度関数 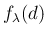 は、
となる。
これが、ポアソン分布の「裏」とはどういうことかを説明するが、
この表現は講義の教科書 [3] によるもので、
一般的な表現かどうかは知らない。
は、
となる。
これが、ポアソン分布の「裏」とはどういうことかを説明するが、
この表現は講義の教科書 [3] によるもので、
一般的な表現かどうかは知らない。
3 節で述べたように、ポアソン分布実は教科書はこの逆の形で書いてあるのであるが、 この形のものもどこかの本に書いてあった (図書館にあった本だと思うが、 どの本かは忘れてしまった)。が、 1 時間の間にある事象が起きる回数の分布になっているとき、 その事象と次に起きた事象の間の時間
は、指数分布
に 従う。
これについて講義では、その本に書いてあった、以下のような説明を行った。
に対して、時間間隔
が
よりも大きい確率
は、
時間の間に 1 回も起こらない確率に等しい。
時間の間に起きる回数
は
に従う (前節の結果) ので、
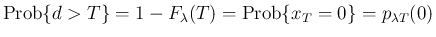
となり、よって
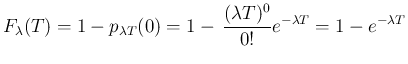
となる。ただ、この説明では若干
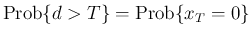 のところが
気になる。
むしろ、これは、次のように考えた方がわかりやすいような気がする。
のところが
気になる。
むしろ、これは、次のように考えた方がわかりやすいような気がする。
最後にその事象が起きた時刻を 0 として、そこからあとは上の計算と同じである。 「最後にその事象が起きた時刻を 0」とすることで、 どこに起点を置いて考えるか、どの時間間隔を見るかが明確になって、 わかりやすくなるように思う。 そしてこれなら時間までの間 に 1 回でも起きれば、この
時間の間には少なくとも 1 回以上 起きることになるが、これは、最初の事象までの時間間隔で考えれば、
を意味し、一方起きる回数
で言えば
を意味する。 よって、
となり、 これを 1 から引けば、
となる。
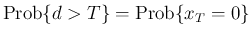 もある程度納得できると
思う。
もある程度納得できると
思う。
竹野茂治@新潟工科大学