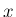 がポアソン分布
がポアソン分布
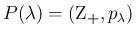 に
従うとすると、
に
従うとすると、
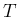 時間 (
時間 (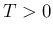 ) にその事象が起きる回数
) にその事象が起きる回数 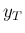 は、
は、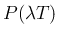 に
従う。
に
従う。
1 時間の間にある事象が独立にいくつか起きるときに、 その事象の起きる回数実際、講義ではこれを証明なしに認めた上で、 ポアソン分布の裏が指数分布となることを簡単に紹介した。がポアソン分布
に 従うとすると、
時間 (
) にその事象が起きる回数
は、
に 従う。
本節では、これをいくつかの段階に分けて示していく。
まず、求めるべき 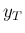 の従う分布を
の従う分布を
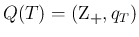 と書くことにする。
目標は、
と書くことにする。
目標は、
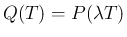 を示すことである。
を示すことである。
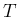 が正の整数
が正の整数 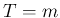 の場合、最初の 1 時間に起きる回数を
の場合、最初の 1 時間に起きる回数を 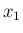 ,
次の 1 時間に起きる回数を
,
次の 1 時間に起きる回数を 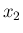 , ...,
最後の 1 時間に起きる回数を
, ...,
最後の 1 時間に起きる回数を 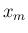 とすれば、
とすれば、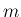 時間で起きる回数は
時間で起きる回数は
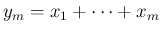 となるので、
となるので、
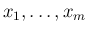 の独立性と、
2 節の例 4 より
の独立性と、
2 節の例 4 より
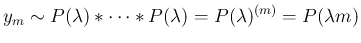
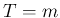 の場合には
の場合には
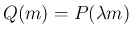 が成り立つ。
が成り立つ。
次は、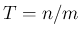 の有理数の場合を考える。
この場合は、逆に
の有理数の場合を考える。
この場合は、逆に 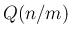 を
を 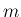 回繰り返せば
回繰り返せば 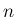 時間の回数となるので、
時間の回数となるので、
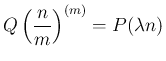
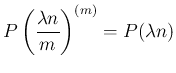
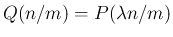 が成り立つ。
が成り立つ。
最後は実数 (無理数) 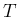 の場合であるが、
の場合であるが、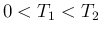 に対しては、当然
に対しては、当然
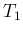 時間に起きる回数よりも
時間に起きる回数よりも 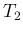 時間に起きる回数の方が多いので、
時間に起きる回数の方が多いので、
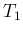 時間に
時間に 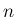 回以上起きる確率よりも、
回以上起きる確率よりも、
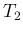 時間に
時間に 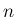 回以上起きる確率の方が多くなる。
なお、「
回以上起きる確率の方が多くなる。
なお、「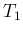 時間に丁度
時間に丁度 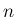 回起きる確率よりも、
回起きる確率よりも、
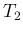 時間に丁度
時間に丁度 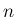 回起きる確率の方が多くなる」とは言えない。
よって、
回起きる確率の方が多くなる」とは言えない。
よって、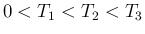 と 0 以上の任意の整数
と 0 以上の任意の整数 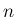 に対して
に対して
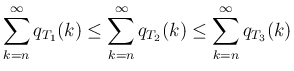
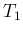 ,
, 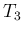 を有理数
を有理数 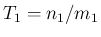 ,
, 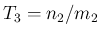 に取り、
に取り、
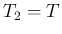 とすると、
とすると、
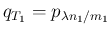 ,
,
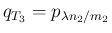 となるので、
となるので、
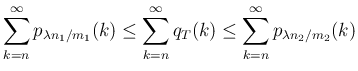
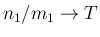 ,
,
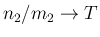 , すなわち
有理数の値を取りながら
, すなわち
有理数の値を取りながら 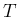 に近付けていくと、
に近付けていくと、
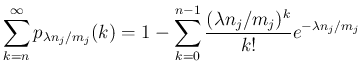
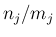 を
を 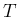 に置きかえたものになり、
よってはさみうちの原理により
に置きかえたものになり、
よってはさみうちの原理により
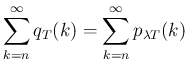
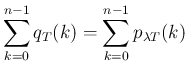
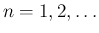 と順番に代入していけば、
すべての
と順番に代入していけば、
すべての 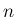 に対して
に対して
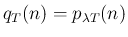 となることがわかる。
となることがわかる。
よって、すべての正の実数 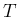 に対して、
に対して、
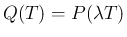 となる
ことが言えたことになる。
となる
ことが言えたことになる。
竹野茂治@新潟工科大学