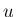 の条件は、
の条件は、
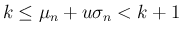 とも書けるが、
これは
とも書けるが、
これは
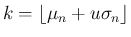 と同値であることに注意する。
そして、各
と同値であることに注意する。
そして、各 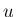 に対して
に対して
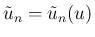 を、
を、
(14) の 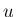 の条件は、
の条件は、
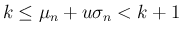 とも書けるが、
これは
とも書けるが、
これは
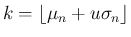 と同値であることに注意する。
そして、各
と同値であることに注意する。
そして、各 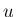 に対して
に対して
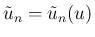 を、
を、
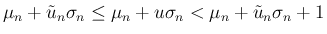
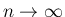 のときに
のときに
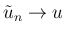 となり、
また
となり、
また
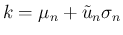 だから、
[1] で
だから、
[1] で
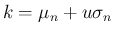 を代入して議論した代わりに
を代入して議論した代わりに
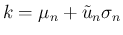 を代入し、
を代入し、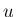 の代わりに
の代わりに 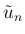 を
用いれば
を
用いれば 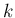 は正しく整数となり、
[1] の議論が正当化できることになる。
それも本節で改めて紹介する。
は正しく整数となり、
[1] の議論が正当化できることになる。
それも本節で改めて紹介する。
本節では、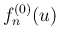 の
の
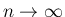 の極限を求める。
の極限を求める。
まず、スターリングの公式
より、ある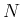 以上の
以上の 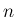 に対しては、
に対しては、
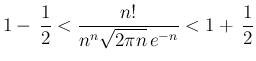
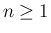 に対して
に対して  を
とすれば、
を
とすれば、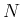 以下の
以下の 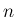 も含め、すべての
も含め、すべての 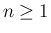 に対し、
となるような
に対し、
となるような 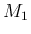 ,
, 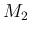 を取ることができ、かつ
となることがわかる。
を取ることができ、かつ
となることがわかる。
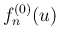 では
では
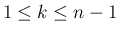 であるが、その
であるが、その 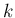 に対して、
に対して、
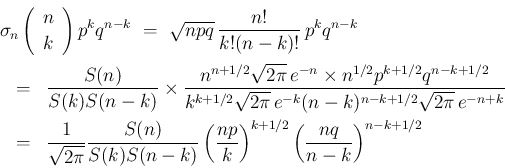
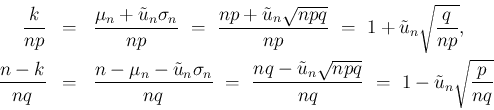
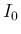 は
は
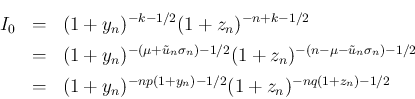
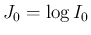 とすると、
となる。これを、
とすると、
となる。これを、
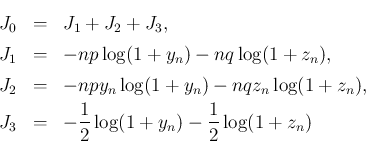
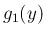 (
(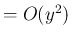 ),
), 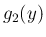 (
(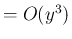 ) を
と定める。ここで、
に注意すると、
) を
と定める。ここで、
に注意すると、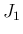 ,
, 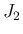 は
は
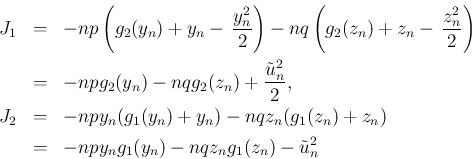
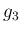 は
とした。
は
とした。
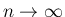 のとき、
のとき、
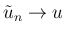 ,
,
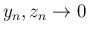 で、
この
で、
この 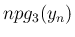 ,
, 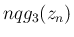 の極限は
の極限は 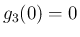 より
不定形となるが、
より
不定形となるが、
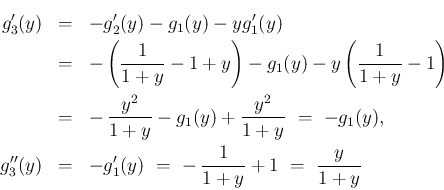
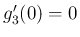 ,
, 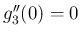 なので、ロピタルの定理より、
なので、ロピタルの定理より、
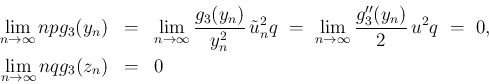
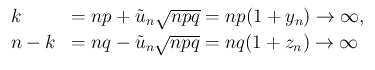
そしてこれが [1] のあいまいな点の修正にもなっている。
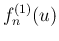 ,
, 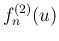 の極限についても見ておく。
まずは
の極限についても見ておく。
まずは
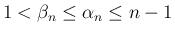 の保証を与えておく。
の保証を与えておく。
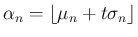 より
より
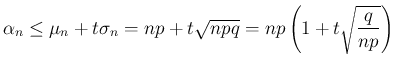
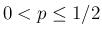 より
より 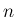 を
を満たすよう大きくとると、(35) の 1 つ目の
不等式から
を
を満たすよう大きくとると、(35) の 1 つ目の
不等式から
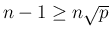 が得られ、2 つ目から
が得られ、2 つ目から
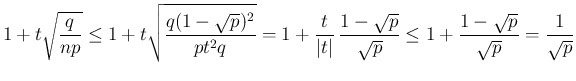
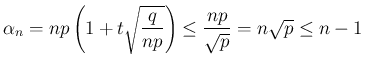
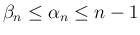 が得られる。
また、
が得られる。
また、
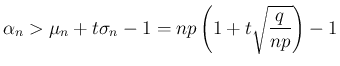
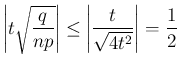
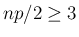 だから、
だから、
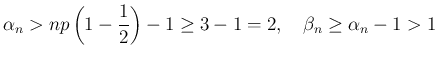
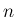 に対しては、
に対しては、
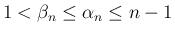 が保証されることになる。
が保証されることになる。
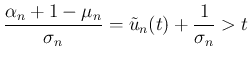
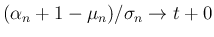 となる。
また、
となる。
また、
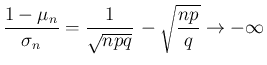
![$\displaystyle \chi_{[(1-\mu_n)/\sigma_n,(\alpha_n+1-\mu_n)/\sigma_n)}(u)
\rightarrow \chi_{(-\infty,t]}(u)
$](img162.png)
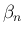 に関しては、(11) より
に関しては、(11) より
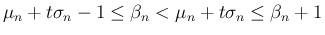
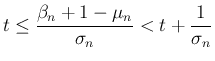
![$\displaystyle \chi_{[(1-\mu_n)/\sigma_n,(\beta_n+1-\mu_n)/\sigma_n)}(u)
\rightarrow \chi_{(-\infty,t]}(u)
$](img166.png)
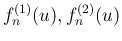 の極限は
となる。
の極限は
となる。
竹野茂治@新潟工科大学