次へ: 5 おわりに
上へ: ある無限級数の値について
前へ: 3 級数の間の等式
(PDF ファイル: series1.pdf)
4 区分求積法
数列の和
は、
と変形すればわかるが、丁度区分求積の公式
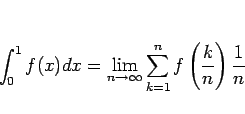 |
(3) |
の右辺が適用できる形をしていて、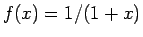 の場合に対応する。
よって、
の場合に対応する。
よって、
となる。
以上で、(1) の値が 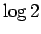 であることが
示されたことになる。
であることが
示されたことになる。
次へ: 5 おわりに
上へ: ある無限級数の値について
前へ: 3 級数の間の等式
竹野茂治@新潟工科大学
2006年4月25日
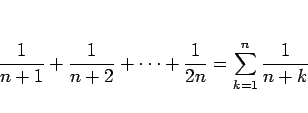
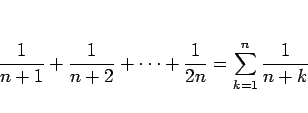
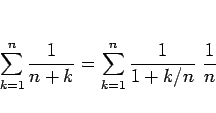
![\begin{eqnarray*}\lim_{n\rightarrow}S_{2n}
&=&
\lim_{n\rightarrow}\sum_{k=1}^n...
...og (1+x)\right]_{x=0}^{x=1}
=
\log 2-\log1
%\ &=&
=
\log 2\end{eqnarray*}](img19.gif)
![]() であることが
示されたことになる。
であることが
示されたことになる。