次へ: 2 補題 上へ: ある無限級数の値について 前へ: ある無限級数の値について (PDF ファイル: series1.pdf)

1 はじめに

無限級数の和を求めることはかなり難しい問題であり、 テイラー展開やフーリエ級数などを駆使してやっと求まる級数などもあるし、 見かけは簡単な級数なのに今だにその値が簡単な式では表されていない級数もある。

ここでは、次の級数

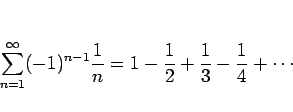$$\sum_{n=1}^\infty (-1)^{n-1}\frac{1}{n} = 1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots$$ (1)

の値を、区分求積の公式を利用して初等的に求める方法を紹介する。

次へ: 2 補題 上へ: ある無限級数の値について 前へ: ある無限級数の値について