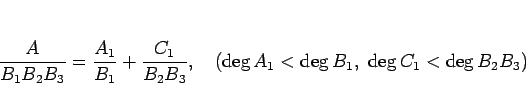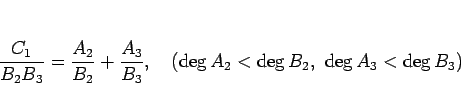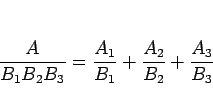![]() 、すなわち
、すなわち ![]() と
と ![]() が互いに素のとき、
ある整式
が互いに素のとき、
ある整式 ![]() ,
, ![]() が存在して、
が存在して、
逆に、このような式が成り立つような
![]() ,
, ![]() が存在する場合は
が存在する場合は
![]() となる。
となる。
左辺が整式に見えて、右辺が 1 というのは奇妙に思うかもしれないが、これは
例えば ![]() ,
, ![]() の場合は、
の場合は、
![]() ,
, ![]() によって
によって
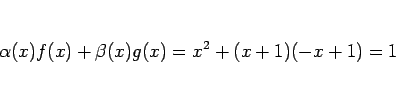
補題 4 の証明
互除法を利用する。
今、![]() ,
, ![]() と書き直して、
と書き直して、
![]() を
を ![]() で割った商を
で割った商を ![]() , 余りを
, 余りを ![]() とすると、
とすると、
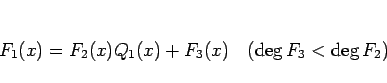
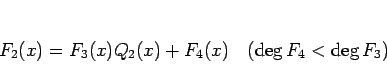
(3) より、
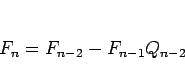
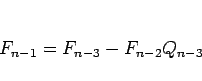
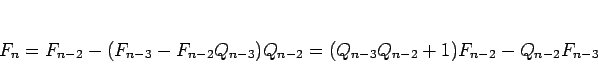
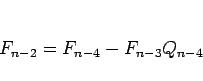
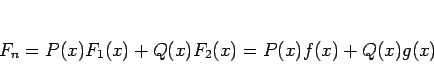
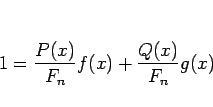
逆に、(2) が成り立つ場合、
![]() として
として
![]() ,
, ![]() を
を ![]() で割った商を
で割った商を ![]() ,
, ![]() とすると、
とすると、
![]() ,
, ![]() なので、
なので、
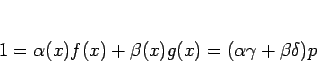
次に、この補題 4 の表現が一意的であることを示す。
補題 4 の ![]() ,
, ![]() は
は
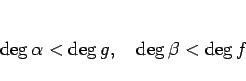
証明
(2) を満たす ![]() ,
, ![]() が
が
![]() のような場合は、
のような場合は、
![]() を
を ![]() で割った商を
で割った商を ![]() ,
余りを
,
余りを
![]() (
(
![]() )
とし、
)
とし、
![]() を
を ![]() で割った商を
で割った商を ![]() ,
余りを
,
余りを
![]() (
(
![]() )
とすれば
)
とすれば
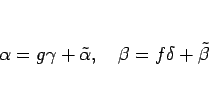
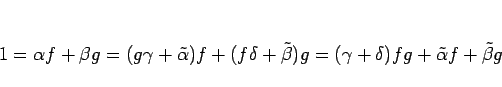
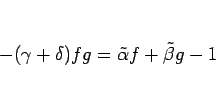
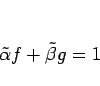
また、1 組しか存在しないことは次のように示される。
もしこのような整式の組が、
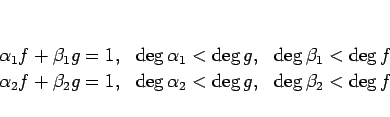
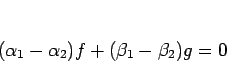
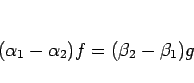
今、もし
![]() ならばこの式の左辺は 0 ではなく、
よって左辺の因子である
ならばこの式の左辺は 0 ではなく、
よって左辺の因子である ![]() は右辺の因子でもなければならないが、
は右辺の因子でもなければならないが、
![]() と
と ![]() は互いに素なので、
は互いに素なので、![]() は
は
![]() の因子で
なくてはならず、
すなわち
の因子で
なくてはならず、
すなわち
![]() は
は ![]() で割り切れなくてはならない
(因数分解の一意性)。
で割り切れなくてはならない
(因数分解の一意性)。
しかし、
![]() だから、それは
だから、それは
![]() を意味する。
そしてそれは
を意味する。
そしてそれは
![]() をも意味するので、
「
をも意味するので、
「
![]() ならば」としたことに矛盾する。
よって、背理法により
ならば」としたことに矛盾する。
よって、背理法により
![]() であることになる。
そしてそれにより
であることになる。
そしてそれにより
![]() となり、
結局
となり、
結局
![]() ,
,
![]() となるので、
2 組は同じものになる。
となるので、
2 組は同じものになる。
この 2 つの補題 4, 5 から、 次の系 6 が導かれる。
![]() のとき、
のとき、
![]() である任意の
整式
である任意の
整式 ![]() に対して、
ある整式
に対して、
ある整式 ![]() ,
, ![]() が存在して、
が存在して、
証明
これは、(2) の両辺を ![]() 倍して、
倍して、
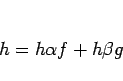
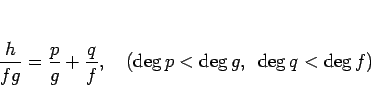
系 2 は、定理 1 を繰り返し使えば得られる。
例えば、![]() のときは、
のときは、
![]() と
と ![]() は互いに素なので、
は互いに素なので、