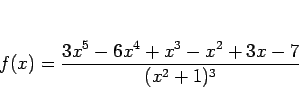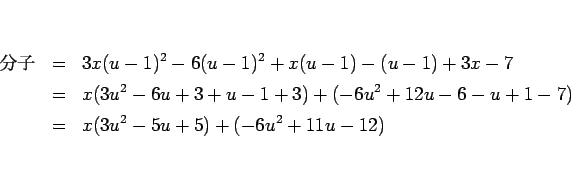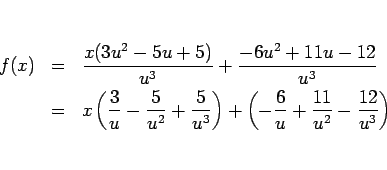次へ: 3 積分の実行
上へ: '有理関数の積分について (その 2)'
前へ: 1 はじめに
(PDF ファイル: quotef2.pdf)
2 奇数次と偶数次の分離について
[1] では、(1) の分子を
奇数次と偶数次の項に分離して、奇数次の方は 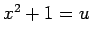 、
偶数次の方は
、
偶数次の方は 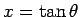 と置換するか、
または部分積分を利用する方法を紹介している。
と置換するか、
または部分積分を利用する方法を紹介している。
しかし、いずれにせよ
の形に直すのであるから、まずそのように整理するのがよいだろうと思う。
よって、まず、
「分子に 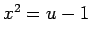 を代入して、それを展開して
を代入して、それを展開して 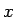 の一次式に整理する」
の一次式に整理する」
ということを行う。
ただし、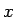 の奇数次の項には、
の奇数次の項には、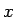 を一つだけ残して、
他の偶数次部分にのみ代入することとする。
それにより、分子は
を一つだけ残して、
他の偶数次部分にのみ代入することとする。
それにより、分子は 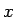 に関する 1 次式となる。
に関する 1 次式となる。
以下、
を例に取って計算する。
よって、
となる。
次へ: 3 積分の実行
上へ: '有理関数の積分について (その 2)'
前へ: 1 はじめに
竹野茂治@新潟工科大学
2006年6月2日
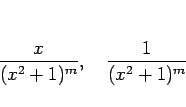
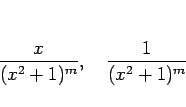
を代入して、それを展開して
の一次式に整理する」