次へ: 2 奇数次と偶数次の分離について 上へ: '有理関数の積分について (その 2)' 前へ: '有理関数の積分について (その 2)' (PDF ファイル: quotef2.pdf)

1 はじめに

以前、有理関数の積分ででてくる一番難しいものの積分

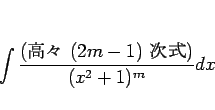$$\int\frac{\mbox{(高々 $(2m-1)$\ 次式)}}{(x^2+1)^m}dx$$ (1)

の積分についてまとめた ([1]) が、 原理的にはその説明の通りなのであるが、 このような積分が出てきたらこうすればよい、 というつきつめた話なので、 実際の計算であの手順を行なおうとすると無駄が起こることもあるし、 帰着させる部分の計算が割と面倒な場合もある。

そこで、具体的な計算を行うことを考えて、 なるべく手間のかからなそうな方法について考察することにする。

次へ: 2 奇数次と偶数次の分離について 上へ: '有理関数の積分について (その 2)' 前へ: '有理関数の積分について (その 2)'