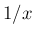
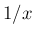 の導関数を必要とするので、
通常の講義で 1 変数関数の商の導関数の説明に使うのは無理であるが、
計算は 5 節の積と合成関数の説明よりも少し簡単になる。
の導関数を必要とするので、
通常の講義で 1 変数関数の商の導関数の説明に使うのは無理であるが、
計算は 5 節の積と合成関数の説明よりも少し簡単になる。
まず、2 変数関数 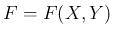 に対して、それに
に対して、それに 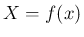 ,
, 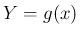 を
代入した合成関数
を
代入した合成関数
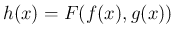 の導関数は、
の導関数は、
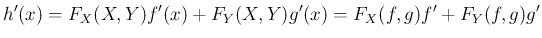
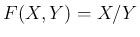 の場合を考えると、
の場合を考えると、
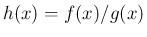 であり、
であり、
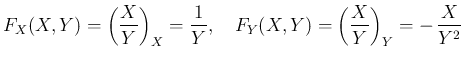
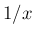 の微分を使用している。これにより、
の微分を使用している。これにより、
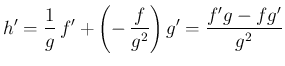
2 変数関数によって分子と分母を別々に考えることができ、 5 節の積の微分の部分が必要なくなり 少し計算が易しくなるが、実質的には同じことをやっていることになる。
竹野茂治@新潟工科大学