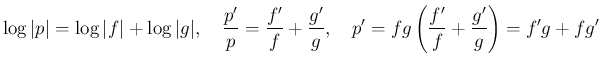6 対数微分法による証明
次に、対数微分法による証明を紹介する。
これは対数の導関数、合成関数の微分法を必要とするが、
それらは商の微分とは独立に説明できるので、
この方法も一応意味はある。
とすると、
なので、この両辺を微分すると合成関数の微分により、
となり、よって両辺 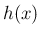 倍すれば、
倍すれば、
となる。
なお、この手法は、積の微分の証明にも使え、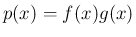 とすれば、
とすれば、
となるが、これを商の場合と比較すると、
積の微分と商の微分の形の類似性の理由や、
真ん中の符号の違いが対数法則から来ることなども見えてくるので、
それなりに悪くない証明方法だと思う。
竹野茂治@新潟工科大学
2020-10-21
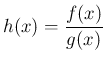
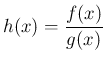
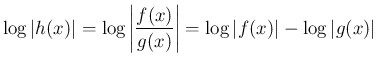
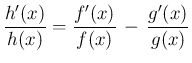
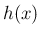 倍すれば、
倍すれば、
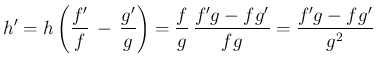
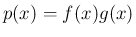 とすれば、
とすれば、