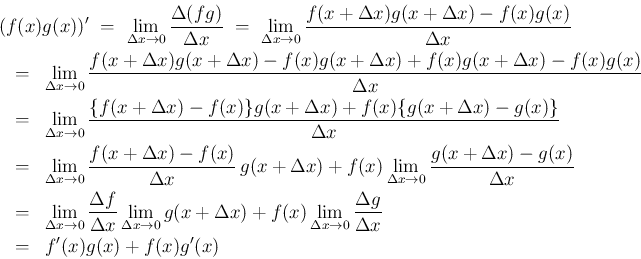
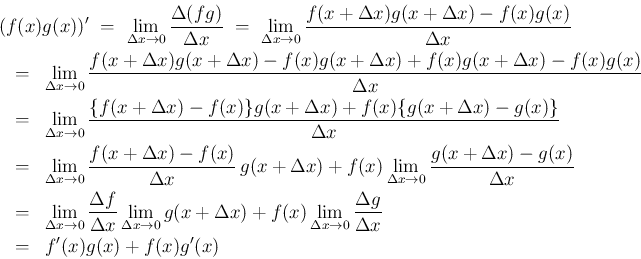
この証明の鍵は、2 行目の部分の真ん中で、
分子に
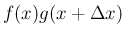 を引いてそして同じものを足す (結果として
増減なし)、という式を追加することで、
分子に
を引いてそして同じものを足す (結果として
増減なし)、という式を追加することで、
分子に 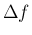 ,
, 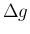 を作り、
そこから積の微分の式が得られているのであるが、
これは初学者には思いつかない技巧的な方法で、
自然に積の微分の公式が得られる、という方法ではないように思う。
を作り、
そこから積の微分の式が得られているのであるが、
これは初学者には思いつかない技巧的な方法で、
自然に積の微分の公式が得られる、という方法ではないように思う。
なお、この証明は、むしろ定義 (3) の式を用いた方が 式としては見やすくなる。
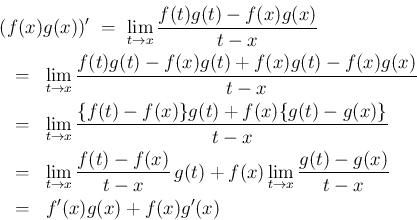
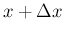 (教科書の場合は
(教科書の場合は 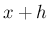 ) が出てこないので、
少し式自体が短くなり見やすいだろう。
) が出てこないので、
少し式自体が短くなり見やすいだろう。
竹野茂治@新潟工科大学