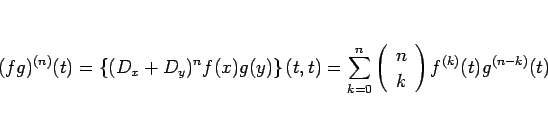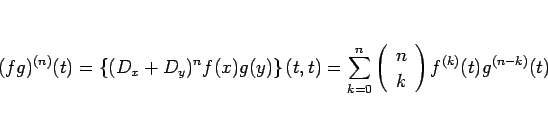3 おわりに
この証明も実は、(7) を示すには、
正確には帰納法を必要とするのであるが、
(7) はまさに 2 項定理による展開であり、
これが成り立つことはある程度自然に見えるので、
そう考えると、むしろこの (6) と (7) の
部分、すなわち、
という変形が、(1) と (2) が
似た形になる理由であると説明できるように思える。
このような説明は、もちろん偏微分を説明した後にしか行えないが、
上のような意味でそれなりに意義のある説明ではないかと思う。
竹野茂治@新潟工科大学
2006年12月27日