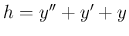
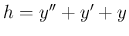 に対する (2) から考えてみる。
に対する (2) から考えてみる。
この (2) は、
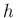 が 1 回微分して元に戻る関数であることを意味するので、
[1] により、
が 1 回微分して元に戻る関数であることを意味するので、
[1] により、
次に、
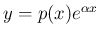 とおいて、(4) に代入すると、
とおいて、(4) に代入すると、
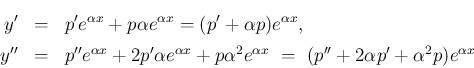
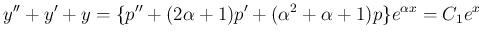
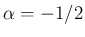 ととると
ととると 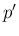 の項が消えて、
となる。
この方程式を満たす
の項が消えて、
となる。
この方程式を満たす 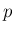 を求めるために、[1] の 6 節と
同様の変形を行う。
を求めるために、[1] の 6 節と
同様の変形を行う。
定数 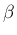 に対して、
に対して、
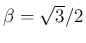 に対して
となることがわかる。
に対して
となることがわかる。
これを積分していけばよいのであるが、右辺の積分はあまり易しくない。 微分で考えると、
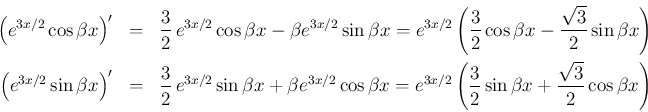
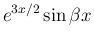 を消去すれば、
を消去すれば、
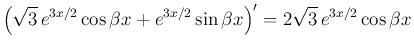

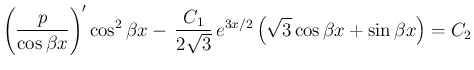
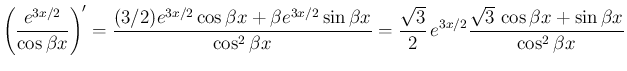
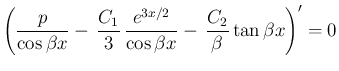
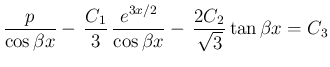
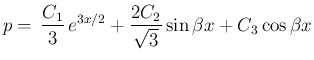
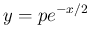 より、
が得られる。
つまり、(1) の解は、
の線形結合であることになる。
最初のものは 1 回の微分で元に戻るので、
実質的には後者 2 つが 3 回微分して元に戻る関数である。
より、
が得られる。
つまり、(1) の解は、
の線形結合であることになる。
最初のものは 1 回の微分で元に戻るので、
実質的には後者 2 つが 3 回微分して元に戻る関数である。
なお、もしこの最終的なおおまかな形を知っていれば、 あるいはこのような形ではないかと予想がつけば、
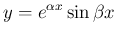
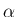 ,
, 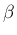 (実数) を求める、
という方法もある。
(実数) を求める、
という方法もある。
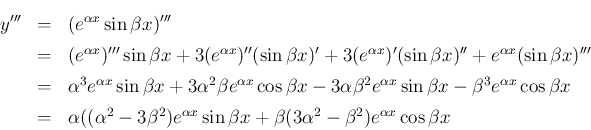
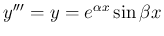 になる。
(11) の後者より
になる。
(11) の後者より
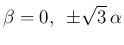
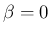 の場合は (11) の
前者より
の場合は (11) の
前者より 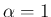 , よって
, よって 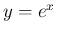 となる。
となる。
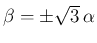 の場合は
の場合は 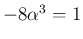 より
より 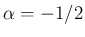 ,
よって
,
よって
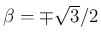 となり、(10) の 2 つ目のものが得られる。
同様に
となり、(10) の 2 つ目のものが得られる。
同様に
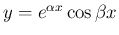 とすれば (10) の 3 つ目のものが得られる。
とすれば (10) の 3 つ目のものが得られる。
竹野茂治@新潟工科大学