5 順列の符号
この節では、行列式の定義 (3) (またはそれと同等の (5) に現れる順列の符号
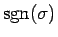 について述べ、4 節で構成した積に
どのように符号をつければいいのかを考える。
について述べ、4 節で構成した積に
どのように符号をつければいいのかを考える。
まず
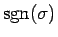 は、[2] では以下のように定義されている:
は、[2] では以下のように定義されている:
順列
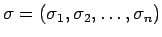 の
各成分の 2 つの組 (
の
各成分の 2 つの組 (
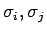 ) (
) (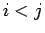 ) のうち、
大小関係が反対になっている (
) のうち、
大小関係が反対になっている (
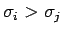 ) ものを
転倒 と呼ぶ。この転倒の個数を
) ものを
転倒 と呼ぶ。この転倒の個数を 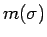 とするとき、
とするとき、
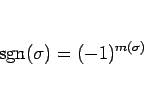 |
(19) |
とする。
例えば、
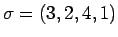 の場合、転倒は
の場合、転倒は
(3,2), (3,1), (2,1), (4,1)
の 4 つなので、
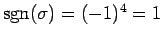 ということになる。
ということになる。
同じことであるが、この順列の符号は、次のような式で定義することもできる:
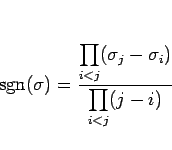 |
(20) |
ここで 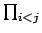 は、
は、
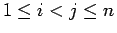 となる
となる 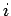 ,
, 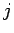 すべての組み合わせに対する積を表わし、よって例えば
すべての組み合わせに対する積を表わし、よって例えば
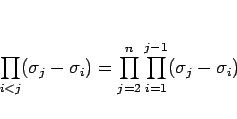
のように書くこともできる。
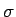 は順列であるから、
この (20) の分子と分母はいずれも
は順列であるから、
この (20) の分子と分母はいずれも
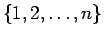 から異なる 2 つの組を
一つずつ選んだものの差の積となっているので、
符号の違いを除けば全く同じものになっていて、
結果としてはこの値は
から異なる 2 つの組を
一つずつ選んだものの差の積となっているので、
符号の違いを除けば全く同じものになっていて、
結果としてはこの値は 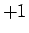 か
か 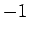 になり、
分子と分母に現われるその組で符号が違っているものが
まさに順列の転倒である 2 つの組に対応するので、
この式の値 (20) が (19) と同じであることが容易にわかる。
になり、
分子と分母に現われるその組で符号が違っているものが
まさに順列の転倒である 2 つの組に対応するので、
この式の値 (20) が (19) と同じであることが容易にわかる。
この順列の符号に対して、次が言える。
補題 6
- (積)
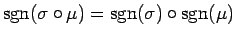
- (部分順列)
![$\sigma=[\mu_1,\mu_2,\ldots,\mu_m]$](img203.gif) に対して、
に対して、
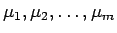 同士の転倒の個数を
同士の転倒の個数を 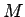 とすると
とすると
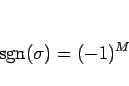
(すなわち、
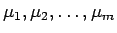 以外のものにはよらない)
以外のものにはよらない)
- (巡回)
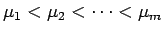 に対して、
に対して、
![$\mathop{\mathrm{sgn}}\nolimits ([\mu_1,\mu_2,\ldots,\mu_m]^{(k)})=(-1)^{k(m-1)}$](img207.gif)
- (反転)
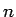 が 4 で割って余りが 0,1 のときは
が 4 で割って余りが 0,1 のときは
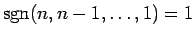 、
、
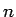 が 4 で割って余りが 2,3 のときは
が 4 で割って余りが 2,3 のときは
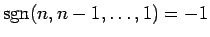
証明
- (20) を利用すれば、
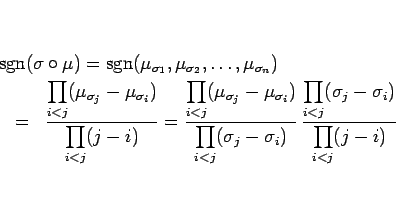
と書けるが、後者の商は
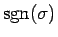 に等しく、
前者も、
に等しく、
前者も、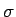 で転倒しているものを
分子と分母で合わせて前後を入れかえれば、結局
で転倒しているものを
分子と分母で合わせて前後を入れかえれば、結局
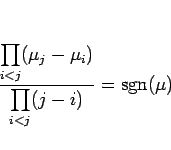
に等しいことがわかる。
-
![$\sigma=[\mu_1,\mu_2,\ldots,\mu_m]$](img203.gif) は、
は、
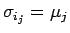 とすれば、
とすれば、
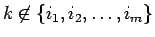 ならば
ならば
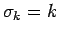 であることを意味する。
であることを意味する。
この動いていない 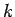 番目の要素に関する転倒の個数を数えてみると、
その転倒は
番目の要素に関する転倒の個数を数えてみると、
その転倒は 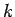 より前にあった
より前にあった 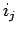 が
が 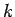 より後ろに行った場合と、
より後ろに行った場合と、
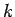 より後ろにあった
より後ろにあった 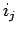 が
が 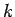 より前に来たものからなる。
しかし、移動前と移動後で
より前に来たものからなる。
しかし、移動前と移動後で 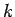 より前のものの個数は
より前のものの個数は 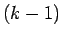 のまま
変わらないから、
のまま
変わらないから、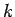 を飛び越えて前に移動したものと後ろに移動したものの
個数は同数となるはずである。
つまり、
を飛び越えて前に移動したものと後ろに移動したものの
個数は同数となるはずである。
つまり、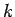 に関する転倒の個数は必ず偶数となる。
に関する転倒の個数は必ず偶数となる。
よって、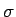 の転倒の個数全体は、
の転倒の個数全体は、
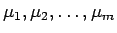 同士の転倒の個数
同士の転倒の個数 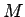 と偶数
と偶数 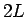 の和となり、
の和となり、
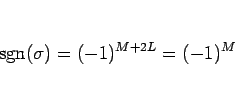
となる。
- 2. より、移動したもの同士の転倒だけを考えればよく、
![\begin{displaymath}[\mu_1,\mu_2,\ldots,\mu_m]^{(1)} = [\mu_2,\mu_3,\ldots,\mu_m,\mu_1]
\end{displaymath}](img217.gif)
の転倒は最後の 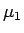 と他のものとの組すべてであるので、
と他のものとの組すべてであるので、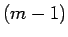 個ある。
よって、
個ある。
よって、
![\begin{displaymath}
\mathop{\mathrm{sgn}}\nolimits ([\mu_1,\mu_2,\ldots,\mu_m]^{(1)})=(-1)^{m-1}
\end{displaymath}](img220.gif) |
(21) |
となり 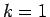 の場合は 3. は成立する。
の場合は 3. は成立する。
一般の 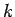 に対しては、補題 1 より
に対しては、補題 1 より
![$[\mu_1,\mu_2,\ldots,\mu_m]^{(k)}$](img221.gif) が
が
![$[\mu_1,\mu_2,\ldots,\mu_m]^{(1)}$](img222.gif) の
の 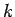 回の積であることから、
上の 1. と (21) により容易に示される。
回の積であることから、
上の 1. と (21) により容易に示される。
-
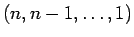 は、すべての組 (
は、すべての組 (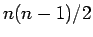 個) が転倒しているので、
個) が転倒しているので、
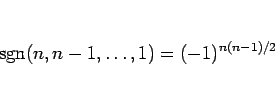
となる。ここで、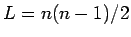 は、
は、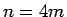 ならば、
ならば、
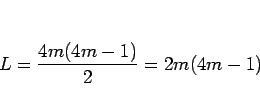
なので偶数である。
以下同様に、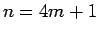 ,
, 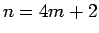 ,
, 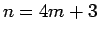 の場合はそれぞれ
の場合はそれぞれ
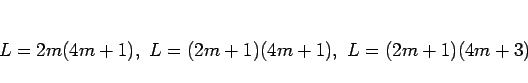
となり、それぞれ、偶数、奇数、奇数であることがわかる。
よって、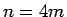 ,
, 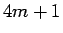 ,
, 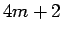 ,
, 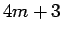 の場合
の場合 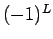 は、
それぞれ
は、
それぞれ 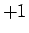 ,
, 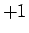 ,
, 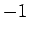 ,
, 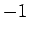 となる。
となる。
この補題 6 を使って、4 節で考察した各項に
どのような符号をつければよいかを考察する。
まずは、各面での斜めの計算について考える。
左上から右下への斜めの方向は
![$[1,2,\ldots,n]^{(j)}$](img236.gif) の巡回順列に対応するので、補題 6 より
の巡回順列に対応するので、補題 6 より
![\begin{displaymath}
\mathop{\mathrm{sgn}}\nolimits ([1,2,\ldots,n]^{(j)})=(-1)^{j(n-1)}
\end{displaymath}](img237.gif)
となる。一方、右上から左下への斜めの積はその反転であるので、
補題 6 より
![\begin{eqnarray*}\mathop{\mathrm{sgn}}\nolimits (\overline{[1,2,\ldots,n]^{(j)}}...
...mits ([1,2,\ldots,n]^{(j)})
\\ &=&
(-1)^{n(n-1)/2}(-1)^{j(n-1)}\end{eqnarray*}](img238.gif)
となる。これを合わせると、これらの積の符号は次のようになる。
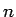 が 4 で割り切れれば、
が 4 で割り切れれば、
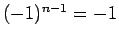 、
、
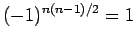 より、
左上から右下への対角線と右上から左下への対角線は
より、
左上から右下への対角線と右上から左下への対角線は 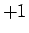 、
その下のものはどちらの方向も一つ下がる度に
、
その下のものはどちらの方向も一つ下がる度に 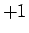 と
と 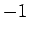 が交互に現われる (2 節の 4 次の計算に対応する)
が交互に現われる (2 節の 4 次の計算に対応する)
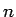 が 4 で割って 1 余る場合は、
が 4 で割って 1 余る場合は、
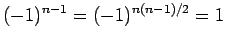 より、
すべての符号が
より、
すべての符号が 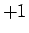 となる
となる
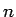 が 4 で割って 2 余る場合は、
が 4 で割って 2 余る場合は、
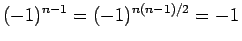 より、
左上から右下への対角線は
より、
左上から右下への対角線は 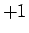 、右上から左下への対角線は
、右上から左下への対角線は 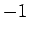 、
その下のものはどちらの方向も一つ下がる度に
、
その下のものはどちらの方向も一つ下がる度に 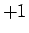 と
と 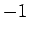 が交互に現われる
が交互に現われる 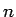 が 4 で割って 3 余る場合は、
が 4 で割って 3 余る場合は、
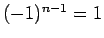 、
、
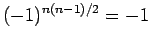 より、
左上から右下への方向の積はすべて
より、
左上から右下への方向の積はすべて 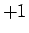 、
右上から左下への方向の積はすべて
、
右上から左下への方向の積はすべて 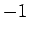 となる (3 次のサラス-関の方法に対応する)
となる (3 次のサラス-関の方法に対応する)
もちろん行の入れ換えによっても符号は変化するが、行の入れ替えの順列は、
4 節により、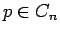 に対して
に対して
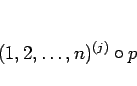
とその反転を行うだけであるから、
符号はその面に対するすべての項の符号が
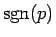 倍されることになる。
つまり、上のような符号のままの計算を各面に対して行い、
その面に対する合計を求めた後でそれに
倍されることになる。
つまり、上のような符号のままの計算を各面に対して行い、
その面に対する合計を求めた後でそれに
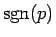 をつければよいことになる。
をつければよいことになる。
さて、
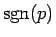 は、
は、
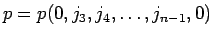 に対して、
補題 6 より、
に対して、
補題 6 より、
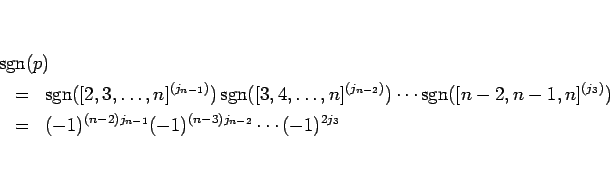
となる。よって、行の巡回の際、
奇数個の行の巡回は符号を変えず、
偶数個の行の巡回 1 回が 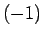 倍に対応する、と数えていけばよいことになる。
倍に対応する、と数えていけばよいことになる。
竹野茂治@新潟工科大学
2008年7月26日
![]() は、[2] では以下のように定義されている:
は、[2] では以下のように定義されている:
の 各成分の 2 つの組 (
) (
) のうち、 大小関係が反対になっている (
) ものを 転倒 と呼ぶ。この転倒の個数を
とするとき、
![]() 番目の要素に関する転倒の個数を数えてみると、
その転倒は
番目の要素に関する転倒の個数を数えてみると、
その転倒は ![]() より前にあった
より前にあった ![]() が
が ![]() より後ろに行った場合と、
より後ろに行った場合と、
![]() より後ろにあった
より後ろにあった ![]() が
が ![]() より前に来たものからなる。
しかし、移動前と移動後で
より前に来たものからなる。
しかし、移動前と移動後で ![]() より前のものの個数は
より前のものの個数は ![]() のまま
変わらないから、
のまま
変わらないから、![]() を飛び越えて前に移動したものと後ろに移動したものの
個数は同数となるはずである。
つまり、
を飛び越えて前に移動したものと後ろに移動したものの
個数は同数となるはずである。
つまり、![]() に関する転倒の個数は必ず偶数となる。
に関する転倒の個数は必ず偶数となる。
![]() の転倒の個数全体は、
の転倒の個数全体は、
![]() 同士の転倒の個数
同士の転倒の個数 ![]() と偶数
と偶数 ![]() の和となり、
の和となり、
![]() に対しては、補題 1 より
に対しては、補題 1 より
![]() が
が
![]() の
の ![]() 回の積であることから、
上の 1. と (21) により容易に示される。
回の積であることから、
上の 1. と (21) により容易に示される。
![]() の巡回順列に対応するので、補題 6 より
の巡回順列に対応するので、補題 6 より
![]() に対して
に対して
![]() は、
は、
![]() に対して、
補題 6 より、
に対して、
補題 6 より、