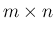
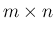 行列
行列
![$A=[a_{ij}]_{m,n}$](img2.png) と
と 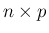 行列
行列
![$B=[b_{ij}]_{n,p}$](img4.png) に
対して、
となる
に
対して、
となる 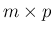 行列
行列
![$[c_{ij}]_{m,p}$](img7.png) として定義される。
として定義される。
つまり 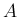 の行ベクトルと、
の行ベクトルと、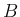 の列ベクトルの内積のような計算を
そのすべての組に対して行って積
の列ベクトルの内積のような計算を
そのすべての組に対して行って積 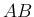 の成分を求めていくのが定義であるが、
実は列ベクトルや行ベクトルを使えば、いくつか簡単な表記、
便利な表記も成り立つことが知られている。
の成分を求めていくのが定義であるが、
実は列ベクトルや行ベクトルを使えば、いくつか簡単な表記、
便利な表記も成り立つことが知られている。
それらは、良く知られていることではあるけれども (初学者は誤解することがあるのでむしろ知らない方がいいかもしれないけれども)、 教科書には記されていないことが多いので、それをここに紹介しておく。
竹野茂治@新潟工科大学