
 の回りの
の回りの 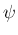 回転の回転変換を、
軸回転行列で表現すること、およびその角の計算について考察する。
回転の回転変換を、
軸回転行列で表現すること、およびその角の計算について考察する。
回転変換を直交行列で表現すること、およびその逆の直交行列から回転変換の 軸と角を求める方法は 5 節で考察し、 直交行列を軸回転行列で表現することは 6 節で考察したが、 回転変換を 6 節のような 3 つの軸回転行列の 合成で表現することは実はそれほど容易ではない。 もちろん、5 節、6 節の話をつなげて、 途中に直交行列を介在することで、回転変換を直交行列で表してそれを 軸回転行列で表すことは原理的には不可能ではないが、 あまり綺麗にはならない。
例えば、6 節の最後に述べた方法で、
回転変換の表現行列 (41) から
軸回転の角 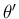 を求めようとすると、
を求めようとすると、
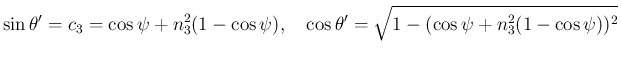
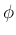 ,
, 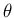 ,
, 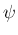 を用いて表すことは可能で、
そしてそれを軸回転角の
を用いて表すことは可能で、
そしてそれを軸回転角の 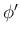 ,
, 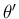 ,
, 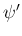 で
表すことは可能だ (解はある) が、その解を表す式は易しくなく、
それらの角同士の関係は綺麗な形にはならない。
で
表すことは可能だ (解はある) が、その解を表す式は易しくなく、
それらの角同士の関係は綺麗な形にはならない。
例えば、逆に (44) から回転変換の
回転軸ベクトル
 を計算することも一応はできるが、
これもあまり綺麗な式にはならない。それを少し紹介する。
(44) の回転軸ベクトルを
を計算することも一応はできるが、
これもあまり綺麗な式にはならない。それを少し紹介する。
(44) の回転軸ベクトルを
 とすると、
とすると、
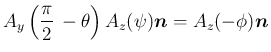
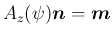 と書くと、
補題 6 より
と書くと、
補題 6 より
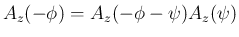 と
なるので、
となる。
と
なるので、
となる。
![$\displaystyle A_y\left(\frac{\pi}{2}\,-\theta\right) - A_z(-\phi-\psi)
=\left[\...
...{1-\cos(\phi+\psi)}&{0}\\
{-\cos\theta}&{0}&{\sin\theta-1}\end{array}\right]
$](img330.png)
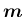 は、
は、
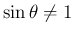 かつ
かつ
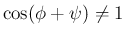 であれば
と書ける (
であれば
と書ける (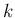 はスカラー)。このとき
はスカラー)。このとき
 は、
は、
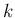 は、
は、
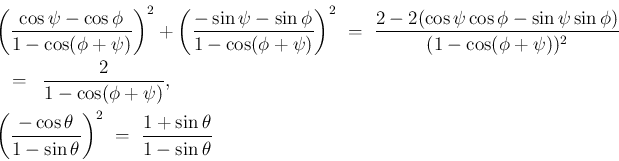
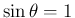 の場合は、
の場合は、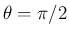 より
より
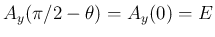 と
なり、
と
なり、
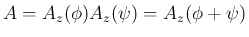
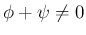 であれば回転軸ベクトルは
であれば回転軸ベクトルは
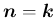 と取れるが、
と取れるが、
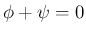 なら
なら 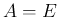 となり回転を表さない。
となり回転を表さない。
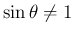 で
で
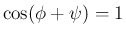 であれば、
であれば、
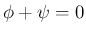 なので、(47) は
なので、(47) は
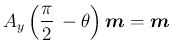
 と取れるから、
と取れるから、
![$\displaystyle \mbox{\boldmath$n$}=A_z(-\psi)\mbox{\boldmath$j$} = \left[\begin{array}{c}{\sin\psi}\\ {\cos\psi}\\ {0}\end{array}\right]
$](img351.png)
(49), (50) により回転軸
ベクトル
 を (46) の
軸回転角
を (46) の
軸回転角
 で表すことができ、
まだ多少の変形は可能ではあるが、
あまり綺麗な形にはならないことがわかるだろう。
つまり、(44) の形と回転変換は
あまり相性がよくない。
で表すことができ、
まだ多少の変形は可能ではあるが、
あまり綺麗な形にはならないことがわかるだろう。
つまり、(44) の形と回転変換は
あまり相性がよくない。
しかし、「3 つの軸回転行列の合成での表現」という制約を取り除けば 回転変換を軸回転行列で表現することは比較的容易である。
回転軸ベクトル
 を
を
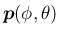 の形で表せば、
図 3 の
の形で表せば、
図 3 の
 の回りの
の回りの 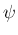 回転は、
回転は、
 を
を
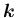 に移動するような回転、
すなわち
に移動するような回転、
すなわち 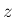 軸に関して
軸に関して 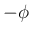 回転して
回転して
 を
を 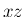 平面に移動し、
次に
平面に移動し、
次に 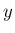 軸に関して (
軸に関して (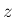 軸から
軸から 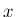 軸方向へ)
軸方向へ)
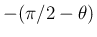 回転
をして、
回転
をして、
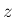 軸に関して
軸に関して 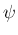 回転して、
回転して、
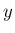 軸に関して
軸に関して
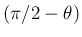 回転してから
回転してから 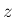 軸に関して
軸に関して 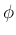 回転
回転
計算はかなり煩雑なので省略するが、 これを展開すると、実際 (51) が (41)、すなわち (40) に 一致することを確認することもできる。
竹野茂治@新潟工科大学