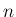 次正方行列に対しては、ケーリー・ハミルトンの公式が成り立つことが
知られている。すなわち、
次正方行列に対しては、ケーリー・ハミルトンの公式が成り立つことが
知られている。すなわち、
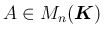 の固有多項式を
の固有多項式を 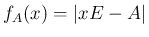 (
(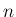 次式) とすると、
次式) とすると、
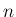 次正方行列に対しては、ケーリー・ハミルトンの公式が成り立つことが
知られている。すなわち、
次正方行列に対しては、ケーリー・ハミルトンの公式が成り立つことが
知られている。すなわち、
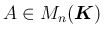 の固有多項式を
の固有多項式を 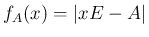 (
(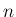 次式) とすると、
次式) とすると、
これにより、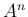 が
が
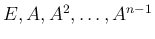 の一次結合、
すなわち
の一次結合、
すなわち 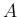 の
の 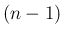 次以下の多項式として表され、
さらに任意の
次以下の多項式として表され、
さらに任意の 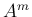 (
(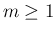 ) も同様に
) も同様に 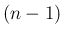 次以下の
次以下の 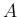 の多項式で
表されることになる。よって、そのような項の無限和である
の多項式で
表されることになる。よって、そのような項の無限和である 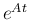 も
も
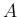 の
の 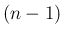 次以下の多項式で表される、
ということが想像されるが、それを考えてみる。
次以下の多項式で表される、
ということが想像されるが、それを考えてみる。
まず、「無限次の多項式」のような解析関数 (ベキ級数) に対する剰余計算 に関する定理を紹介する。
関数が
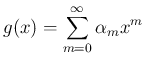
で定義されで収束する解析関数であるとし、
を
次多項式
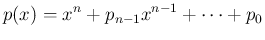
とする。このとき、解析関数なお、(商) と
次以下の 多項式
(余り) が存在して、
が成り立つ。
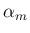 ,
, 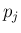 は一般に複素数とする。
は一般に複素数とする。
証明
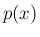 を (
を (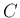 の範囲で) 1 次式の積に因数分解する。
の範囲で) 1 次式の積に因数分解する。
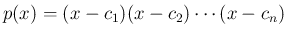
![$\displaystyle q_1(x)
=
\left\{\begin{array}{ll}
\displaystyle \frac{g(x)-g(...
...x\neq c_1$\ のとき})\\ [2ex]
g'(c_1) & (\mbox{$x=c_1$\ のとき})
\end{array}\right. $](img369.png)
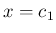 は
は 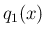 の除去可能特異点で、
の除去可能特異点で、
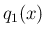 も
も 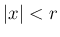 で正則となり、よって
で正則となり、よって 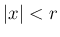 で解析的となる。
そして、
と書ける。
同様に、
で解析的となる。
そして、
と書ける。
同様に、
![$\displaystyle q_2(x)
=
\left\{\begin{array}{ll}
\displaystyle \frac{q_1(x)-...
...neq c_2$\ のとき})\\ [2ex]
q_1'(c_2) & (\mbox{$x=c_2$\ のとき})
\end{array}\right. $](img373.png)
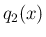 も
も 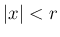 で解析的で、
で解析的で、
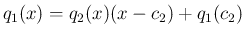
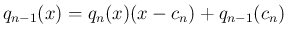
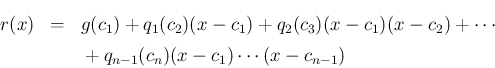
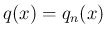 に対して
に対して
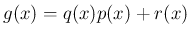 が成り立つ。
が成り立つ。
この定理 8.1 により、
となるような解析関数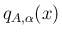 と
と 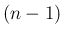 次以下の
多項式
次以下の
多項式
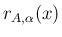 が存在することになる。
が存在することになる。
今、 の固有値を
の固有値を
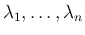 とすると、
とすると、
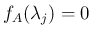 なので、(32) に代入すると
なので、(32) に代入すると
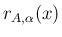 は高々
は高々 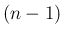 次式であるからその係数は
次式であるからその係数は 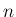 個以下で、
よってもしすべての固有値
個以下で、
よってもしすべての固有値 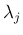 が異なれば、
(33) からその係数を決定でき (
が異なれば、
(33) からその係数を決定でき (
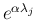 で表され)、
で表され)、
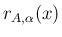 が求まる。
すなわち、未定係数
が求まる。
すなわち、未定係数 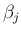 を用いて
を用いて
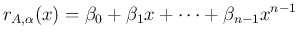
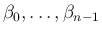 に
対する連立方程式
に
対する連立方程式
![$\displaystyle \left[\begin{array}{cccc}1&\lambda_1&\cdots&\lambda_1^{n-1}\\
\...
...{array}{c}e^{\alpha\lambda_1}\\ \vdots\\ e^{\alpha\lambda_n}\end{array}\right]
$](img389.png)
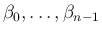 について解けばよい。
ちなみに、この方程式の係数行列はファンデルモンド行列と
呼ばれるものになっていて、
について解けばよい。
ちなみに、この方程式の係数行列はファンデルモンド行列と
呼ばれるものになっていて、
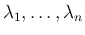 が
すべて異なれば、確かに逆行列が存在し、
が
すべて異なれば、確かに逆行列が存在し、
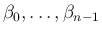 が
求まる。
が
求まる。
次に固有値に重解がある場合を考える。
固有値 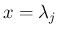 が
が 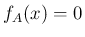 の
の 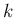 重解である場合、
(33) の方程式のうち
重解である場合、
(33) の方程式のうち 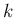 本が 1 本の同じ方程式に
なってしまうが、
この場合
本が 1 本の同じ方程式に
なってしまうが、
この場合 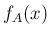 は
は
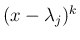 で割り切れるので、
で割り切れるので、
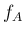 の
の 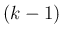 階までの導関数に対して
階までの導関数に対して
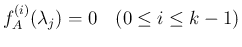
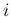 階微分すると (
階微分すると (
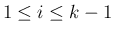 )、
)、
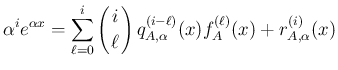
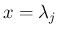 とすると
とすると
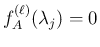 より
となり、これにより足りない
より
となり、これにより足りない  本の方程式が補えることになる。
本の方程式が補えることになる。
以上により、固有値に重解がある場合も含めて
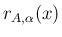 が求められ
ることになり、
そして (32) に
が求められ
ることになり、
そして (32) に 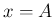 を代入すると、
(30) により
を代入すると、
(30) により
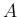 の
の 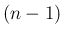 次以下の多項式で表されることになる。
次以下の多項式で表されることになる。
前節で計算した 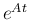 を、この方法で計算してみる。
まずは、
を、この方法で計算してみる。
まずは、
![$\displaystyle A=\left[\begin{array}{cc}0&1\\ -4&0\end{array}\right]
$](img404.png)
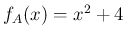 ,
,
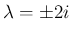 だったので、
だったので、
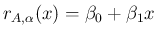 とすると、
(33) は
とすると、
(33) は
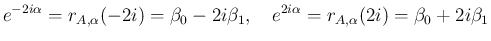
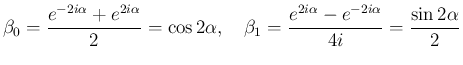
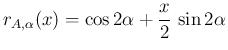
![$\displaystyle e^{\alpha A}
=
r_{A,\alpha}(A)
=
E\cos 2\alpha + \frac{A}{2}\sin...
...{cc}\cos2\alpha &\sin2\alpha/2\\ -2\sin 2\alpha &\cos2\alpha\end{array}\right]
$](img411.png)
次に、
![$\displaystyle A = \left[\begin{array}{cccc}0&0&1&0\\ 0&0&0&1\\ 1&2&0&2\\ 1&-1&3&0\end{array}\right]
$](img412.png)
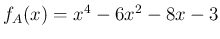 であり、
固有値は
であり、
固有値は 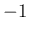 (3 重根) と
(3 重根) と 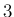 であったので、
であったので、
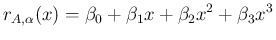
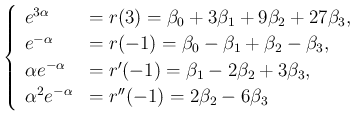
![$\displaystyle \left[\begin{array}{cccc}1&3&9&27\\ 1&-1&1&-1\\ 0&1&-2&3\\ 0&0&2&...
...ha}\\ e^{-\alpha}\\ \alpha e^{-\alpha}\\ \alpha^2e^{-\alpha}\end{array}\right]
$](img417.png)
 を含まない数だけの計算にするために、
この係数行列
を含まない数だけの計算にするために、
この係数行列 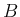 の逆行列を消去法で計算する。
これも一応分数を出さないように計算してみる。
の逆行列を消去法で計算する。
これも一応分数を出さないように計算してみる。
![\begin{eqnarray*}\lefteqn{[B\ \vert\ E]
\ =\
\left[\begin{array}{cccc\vert cc...
...0\\ 0&0&64&0 &3&-3&-12&8\\ 0&0&0&64 &1&-1&-4&-8\end{array}\right]\end{eqnarray*}](img419.png)
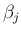 が求まる。この
が求まる。この 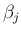 に対して
に対して
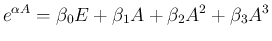
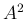 ,
, 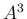 を計算すればよい。
を計算すればよい。
![\begin{eqnarray*}A^2
&=&
\left[\begin{array}{cccc}0&0&1&0\\ 0&0&0&1\\ 1&2&0&2\...
...cccc}2&-2&7&2\\ 3&6&1&5\\ 9&12&8&12\\ 6&-3&18&8\end{array}\right]\end{eqnarray*}](img426.png)
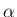 によらない定数行列
によらない定数行列 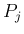 により
により
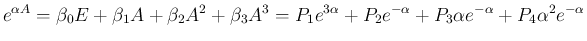
![\begin{eqnarray*}\lefteqn{64P_1
=
E+3A+3A^2+A^3}
\\ &=&\hspace{-.8em}
\left...
...ccc}2&4&-2&0\\ -2&-4&2&0\\ -2&-4&2&0\\ 2&4&-2&0\end{array}\right]\end{eqnarray*}](img430.png)
こちらの計算では、固有ベクトル、広義固有ベクトルの計算はないが、
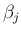 を求める連立方程式の計算と
を求める連立方程式の計算と 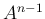 の計算が必要で、
さらに
の計算が必要で、
さらに 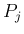 による表現を求める場合は (37) の行列の
定数倍の和の計算が必要になる。
理論展開にはジョルダン標準形の方が良いかもしれないが、
具体的な
による表現を求める場合は (37) の行列の
定数倍の和の計算が必要になる。
理論展開にはジョルダン標準形の方が良いかもしれないが、
具体的な 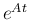 の計算をするには、
こちらのケーリー・ハミルトンの公式を利用する方が最終目的にも少し近く、
計算もやや易しい気がする。
の計算をするには、
こちらのケーリー・ハミルトンの公式を利用する方が最終目的にも少し近く、
計算もやや易しい気がする。
なお、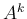 を経由せずに直接
を経由せずに直接 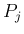 が計算できればもっと楽になるが、
そのような計算法があるかどうかまではわからなかった。
が計算できればもっと楽になるが、
そのような計算法があるかどうかまではわからなかった。
竹野茂治@新潟工科大学