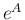
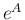 を定義する。
を定義する。
に対し、
を、
の無限級数で定義する。ただし、この定義は、(
でも) とする。
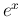 のマクローリン展開を行列に拡張したものになっているが、
(1) の具体的な計算にも
のマクローリン展開を行列に拡張したものになっているが、
(1) の具体的な計算にも 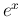 のマクローリン展開が
用いられる。
のマクローリン展開が
用いられる。
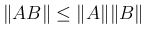 より、
より、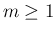 に対して
に対して
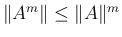 が
成り立ち、
が
成り立ち、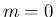 に対しては、
に対しては、
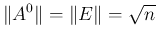
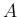 に対し常に絶対収束し、
に対し常に絶対収束し、
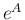 は正しく定義されることになる。
は正しく定義されることになる。
なお、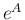 には別の表現式 (別の定義) もある。それは、
には別の表現式 (別の定義) もある。それは、
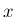 に対する
に対応する。
なお、余談だが、(4) は実数の
に対する
に対応する。
なお、余談だが、(4) は実数の 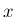 だけでなく
複素数に対しても成立し、すなわち
となることが言え、
いわゆる「オイラーの公式」の別な「証明」(根拠) にもなっている (cf. [3])。
だけでなく
複素数に対しても成立し、すなわち
となることが言え、
いわゆる「オイラーの公式」の別な「証明」(根拠) にもなっている (cf. [3])。
定理 3.2
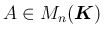 に対して (3) が成り立つ。
に対して (3) が成り立つ。
証明
(3) の右辺のカッコの式の 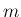 乗を展開して
乗を展開して
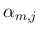 は、
は、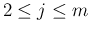 に対して、
に対して、
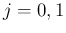 に対しては、
に対しては、
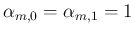 となる。
となる。
なお、(7) の最後の式で 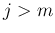 とすると、
積に
とすると、
積に 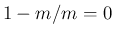 が含まれるので 0 となり、
よってそれをもって
が含まれるので 0 となり、
よってそれをもって 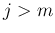 に対して
に対して
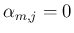 と定める。
このとき、
と定める。
このとき、
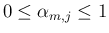 や、
や、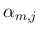 が
が 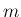 に
関して増加、
に
関して増加、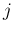 に関して減少であること、および固定した
に関して減少であること、および固定した 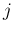 に対して
に対して
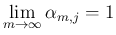
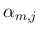 により、
(6) は
と無限級数としても表現されることになるが、
これは (2) が優級数になっているので絶対収束する。
この (8) の
により、
(6) は
と無限級数としても表現されることになるが、
これは (2) が優級数になっているので絶対収束する。
この (8) の 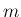 に関する極限が
に関する極限が 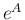 であることを示す。
となるが、この (9) の最後の右辺を
であることを示す。
となるが、この (9) の最後の右辺を 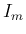 と
書くことにすると、
と
書くことにすると、
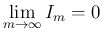 を示せばよい。
を示せばよい。
大きな自然数 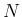 に対し、
に対し、
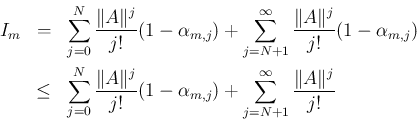
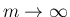 とすれば、
左辺は極限が存在するとは (まだ) 限らないが、
とすれば、
左辺は極限が存在するとは (まだ) 限らないが、
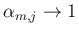 より
が成り立つ (左辺は上極限)。
より
が成り立つ (左辺は上極限)。
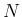 は任意で、左辺は
は任意で、左辺は 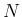 によらないので、
によらないので、
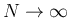 とすれば (10) の右辺
は 0 に収束し、よって左辺の上極限は 0 となり、
とすれば (10) の右辺
は 0 に収束し、よって左辺の上極限は 0 となり、
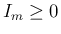 より
より
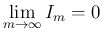 が示されたことになる。
が示されたことになる。
竹野茂治@新潟工科大学