6 行列の積
帰納的な行列式の定義の場合、一番厄介なのは「行列式の積が、積の行列式」
になるという性質の証明であろう。
この事実を、帰納法が使えるように拡張した形で証明する。
まず、次のような記法を導入する。
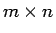 行列
行列 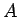 に対し、
に対し、
-
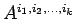 =
= 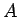 の
の 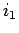 行,
行, 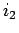 行,...,
行,..., 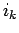 行を
上から順に並べた
行を
上から順に並べた 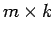 行列
行列
-
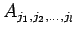 =
= 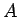 の
の 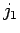 列,
列, 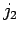 列,...,
列,..., 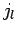 列を
左から順に並べた
列を
左から順に並べた 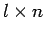 行列
行列
-
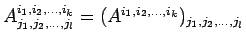 (
(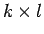 行列)
行列)
例えば、
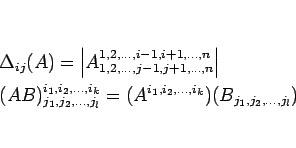
となることに注意せよ。
また、多重数列
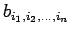 に対して、
に対して、
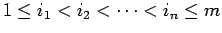 となる
となる
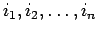 すべて
の組合せに対する和
すべて
の組合せに対する和
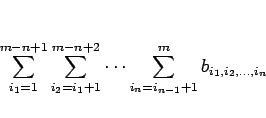
を、簡単に
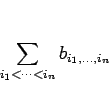
と書くことにする。このとき、
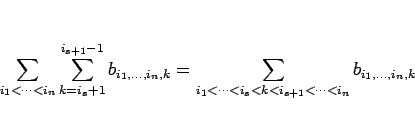 |
(15) |
が成り立つ。簡単のため、 ,
, 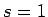 の場合を考えれば、
の場合を考えれば、
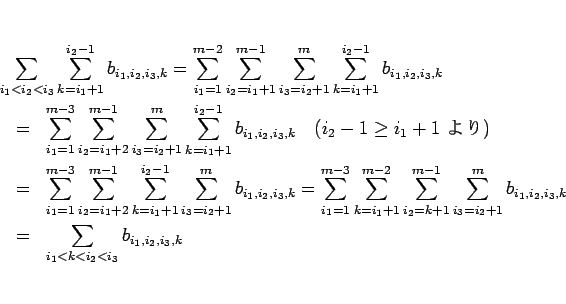
のようになるからである。同様に、
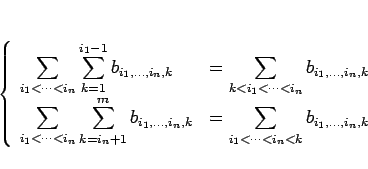 |
(16) |
も成り立つ。
この節では、以下の定理を示す。
定理 7
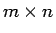 行列
行列 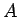 と
と 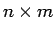 行列 B に対して、
行列 B に対して、
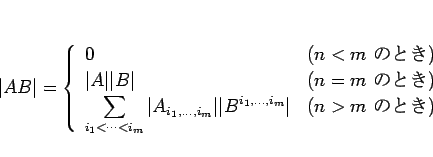 |
(17) |
これを、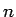 を固定して、
を固定して、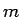 に関する帰納法で証明する。
に関する帰納法で証明する。
まず、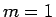 のときは、
のときは、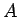 は
は 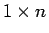 行列、
行列、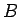 は
は 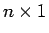 行列なので、
行列なので、
![\begin{eqnarray*}\vert AB\vert
&=&
\left\vert[a_{11}\cdots a_{1n}]\left[\begin...
...n a_{1i}b_{i1}
\\ &=&
\sum_{i=1}^n \vert A_i\vert\vert B^i\vert\end{eqnarray*}](img105.gif)
となるので確かに成り立つ。
よって 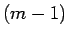 までは成り立つとして
までは成り立つとして 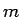 の場合を示す。
の場合を示す。
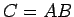 とすると
とすると  は
は 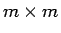 行列なので、
行列なので、
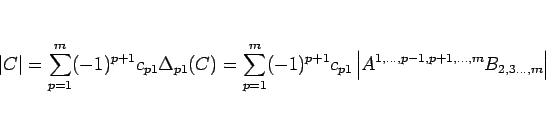
となるが、
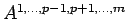 は
は 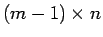 行列、
行列、
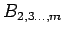 は
は 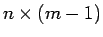 行列なので、
この積の行列式には帰納法の仮定を適用できる。
まず
行列なので、
この積の行列式には帰納法の仮定を適用できる。
まず 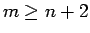 、すなわち
、すなわち 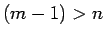 の場合は
の場合は
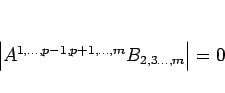
となるので、よって 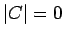 が言える。
が言える。
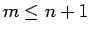 の場合は、
の場合は、
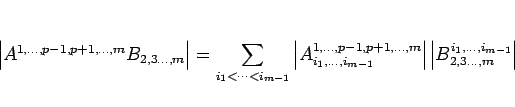
となる。ここで、
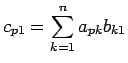 より、
より、
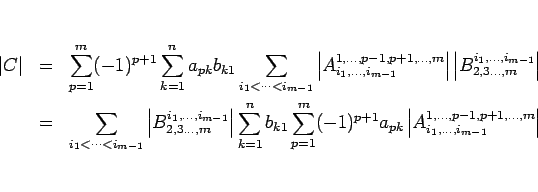
となるが、
![\begin{displaymath}
\left\vert A^{1,\ldots,p-1,p+1,\ldots,m}_{i_1,\ldots,i_{m-1}...
...m-1}}\right]\right)
\hspace{1zw}(\mbox{$\ast$\ は任意の 1 列})
\end{displaymath}](img123.gif)
と見ることもできるので、よって、
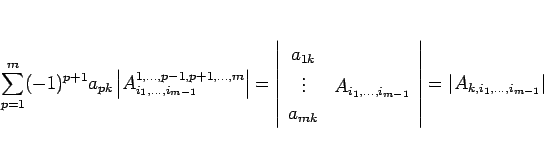
となり、
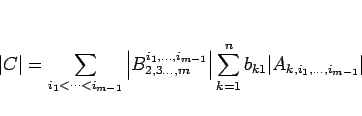 |
(18) |
となる。
ここで、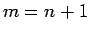 の場合は、
の場合は、
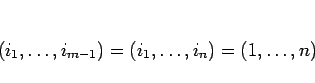
となるので、
![\begin{displaymath}
\vert A_{k,i_1,\ldots,i_{m-1}}\vert=\vert\mbox{\boldmath$a$}...
...{1zw}(A=[\mbox{\boldmath$a$}_1\ \cdots \mbox{\boldmath$a$}_n])
\end{displaymath}](img128.gif)
となり、1 列目の
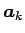 と
と 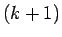 列目が必ず等しくなるので、
よって系 6 より
すべての
列目が必ず等しくなるので、
よって系 6 より
すべての 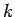 に対して
に対して
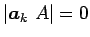 となり、
よって
となり、
よって 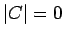 となる。
となる。
よって、後は 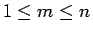 の場合のみ考えればよい。
の場合のみ考えればよい。
上に述べたことと同様に、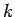 が
が
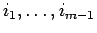 のいずれかと
一致すれば
のいずれかと
一致すれば
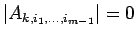 となるので、よって、
となるので、よって、
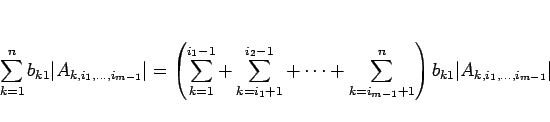 |
(19) |
となる。列の入れ換え (定理 5) を順に行なえば、
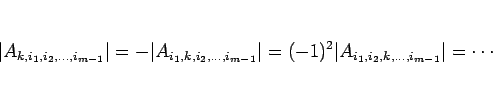
のようになり、よって 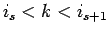 のとき
のとき
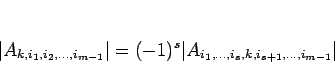
とできるので、(18) に (19) を
代入すれば、
(15), (16)、および
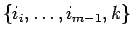 を
を
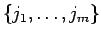 と書くことにより、
と書くことにより、
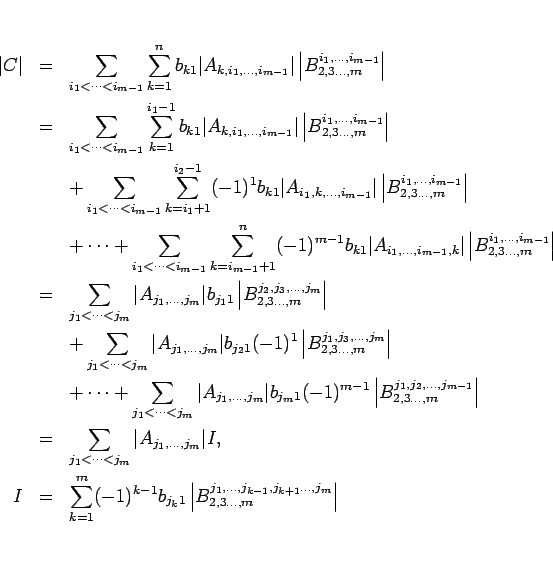
のようにすることができる。この、最後の行列式は、
![\begin{displaymath}
\left\vert B^{j_1,\ldots,j_{k-1},j_{k+1}\ldots,j_m}_{2,3\ldo...
...eft(\left[\ast\ B^{j_1,\ldots j_m}_{2,3\ldots,m}\right]\right)
\end{displaymath}](img142.gif)
なので、
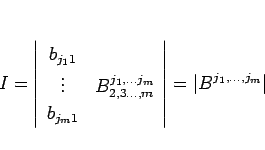
となる。よって、結局、
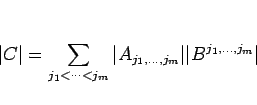
が得られたことになり、これで定理 7 の証明が終了する。
竹野茂治@新潟工科大学
2006年12月8日
![]() 行列
行列 ![]() に対し、
に対し、
![]() に対して、
に対して、
![]() となる
となる
![]() すべて
の組合せに対する和
すべて
の組合せに対する和
![]() 行列
行列 ![]() と
と ![]() 行列 B に対して、
行列 B に対して、
![]() を固定して、
を固定して、![]() に関する帰納法で証明する。
に関する帰納法で証明する。
![]() のときは、
のときは、![]() は
は ![]() 行列、
行列、![]() は
は ![]() 行列なので、
行列なので、
![]() とすると
とすると ![]() は
は ![]() 行列なので、
行列なので、
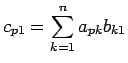 より、
より、
![]() の場合のみ考えればよい。
の場合のみ考えればよい。
![]() が
が
![]() のいずれかと
一致すれば
のいずれかと
一致すれば
![]() となるので、よって、
となるので、よって、