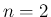
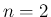 の 2 次の正方行列の場合を考えてみる。
の 2 次の正方行列の場合を考えてみる。
![$\displaystyle A=\left[\begin{array}{cc}a&b\\ c&d\end{array}\right],
\hspace{1zw}
B=\left[\begin{array}{cc}x&y\\ z&w\end{array}\right]
$](img20.png)
![\begin{eqnarray*}AB
&=&
\left[\begin{array}{cc}a&b\\ c&d\end{array}\right]\l...
...left[\begin{array}{cc}ax+cy&bx+dy\\ az+cw&bz+dw\end{array}\right]\end{eqnarray*}](img21.png)
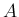 と
と 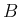 が可換であることは、
が可換であることは、
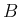 が
が 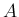 の 1 次式
の形で表されるかどうかを示すことである。
の 1 次式
の形で表されるかどうかを示すことである。
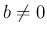 かつ
かつ 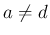 の場合
の場合
この場合、(2) より
となり、 よって (1), (5) より となり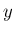 ,
, 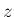 を
を 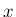 ,
, 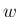 で表せる。
そして (6) が (3) が
得られるので、
この場合は (5), (6) を
満たすことが
で表せる。
そして (6) が (3) が
得られるので、
この場合は (5), (6) を
満たすことが 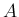 と
と 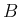 が可換であることと同値となる。
が可換であることと同値となる。
そして、この場合 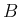 は、
は、
![\begin{eqnarray*}B
&=&
\left[\begin{array}{cc}x&y\\ z&w\end{array}\right]
\ ...
...w}{a-d}\,(A-dE)
\ =\
\frac{x-w}{a-d}\,A + \frac{aw-dx}{a-d}\,E\end{eqnarray*}](img38.png)
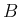 が
が 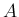 の 1 次式 (4) の
形になることがわかる。
の 1 次式 (4) の
形になることがわかる。
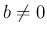 かつ
かつ 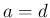 の場合
となる。
の場合
となる。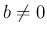 なので、(8) より
となり、(9) は自然に成り立つ。
よってこの場合は、
(7) と (10) が
可換の条件となる。
この場合、
なので、(8) より
となり、(9) は自然に成り立つ。
よってこの場合は、
(7) と (10) が
可換の条件となる。
この場合、
![$\displaystyle A
= \left[\begin{array}{cc}a&b\\ c&a\end{array}\right]
= aE + \left[\begin{array}{cc}0&b\\ c&0\end{array}\right]
$](img44.png)
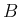 は (7), (10) より、
は (7), (10) より、
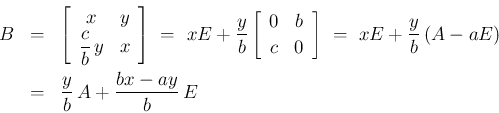
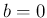 かつ
かつ 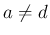 の場合
の場合
この場合は (2) より
となり、また (1) は両辺 0 になり、 (3) は となるので、この (11), (12) が 可換の条件となる。この場合 は、
は、
![$\displaystyle A = \left[\begin{array}{cc}a&0\\ c&d\end{array}\right]
$](img49.png)
 は、(11), (12) より
は、(11), (12) より
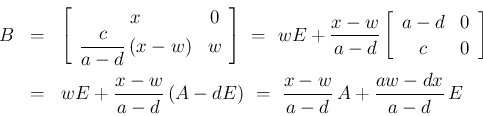
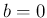 かつ
かつ 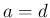 の場合
の場合
この場合、(1) より 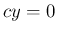 となるが、
となるが、
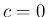 だと
だと 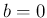 ,
, 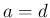 より
より 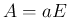 となって仮定に反する。
よって
となって仮定に反する。
よって 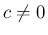 で、
で、
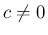 より
となる。この (13), (14) が
可換の条件となる。この場合、
より
となる。この (13), (14) が
可換の条件となる。この場合、
![$\displaystyle A
= \left[\begin{array}{cc}a&0\\ c&a\end{array}\right]
= aE + c\left[\begin{array}{cc}0&0\\ 1&0\end{array}\right]
$](img55.png)
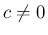 , (13), (14) より、
, (13), (14) より、
![\begin{eqnarray*}B
&=&
\left[\begin{array}{cc}x&0\\ z&x\end{array}\right]
\ =...
... + \frac{z}{c}(A-aE)
\\ &=&
\frac{z}{c}\,A + \frac{cx-az}{c}\,E\end{eqnarray*}](img56.png)
以上をまとめると、
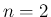 で
で 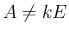 ,
, 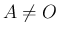 の場合は、
確かに
の場合は、
確かに 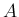 ,
, 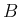 が可換になるのは
が可換になるのは 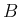 が
が 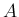 の 1 次式の場合である
ことが示されたことになる。
の 1 次式の場合である
ことが示されたことになる。
竹野茂治@新潟工科大学