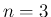
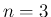 の 3 次の正方行列について考える。
実はこの場合は
の 3 次の正方行列について考える。
実はこの場合は 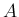 ,
, 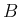 が可換でも、
が可換でも、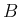 が
が 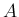 の 2 次式で
書けるとは限らない。すなわち容易に反例が作れる。
の 2 次式で
書けるとは限らない。すなわち容易に反例が作れる。
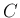 ,
, 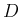 を
を
![$\displaystyle C = \left[\begin{array}{ccc}0&1&0\\ 0&0&0\\ 0&0&0\end{array}\righ...
...space{1zw}
D = \left[\begin{array}{ccc}0&0&0\\ 0&0&0\\ 0&1&0\end{array}\right]
$](img62.png)
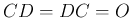 となる。
これも実は反例の一つなのであるが、さらに
となる。
これも実は反例の一つなのであるが、さらに
![$\displaystyle A = E+aC = \left[\begin{array}{ccc}1&a&0\\ 0&1&0\\ 0&0&1\end{arra...
...ce{1zw}
B=bD = \left[\begin{array}{ccc}0&0&0\\ 0&0&0\\ 0&b&0\end{array}\right]
$](img64.png)
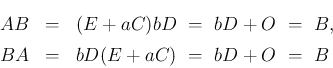
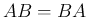 となる。
となる。
しかし、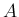 (および
(および 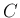 ) は上三角行列なので、
) は上三角行列なので、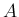 (および
(および 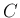 ) の
多項式も (さらに言えば
) の
多項式も (さらに言えば 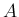 の負のべきも) すべて上三角行列となる。
一方
の負のべきも) すべて上三角行列となる。
一方 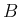 (および
(および 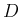 ) は下三角行列なので、
) は下三角行列なので、
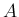 (および
(および 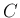 ) の多項式で表わされることはない。
) の多項式で表わされることはない。
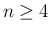 の場合も、容易に
の場合も、容易に 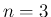 の場合と同じ形の反例が作れるので、
結局
の場合と同じ形の反例が作れるので、
結局 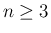 では
では 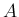 ,
, 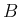 が可換であっても
が可換であっても 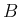 が
が 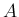 の
多項式で表されるとは限らないことになり、
可換ならば
の
多項式で表されるとは限らないことになり、
可換ならば 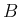 が
が 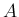 の多項式で表されるのは
の多項式で表されるのは 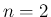 の場合のみ、
ということになる。
の場合のみ、
ということになる。
竹野茂治@新潟工科大学