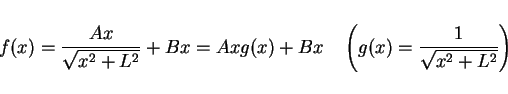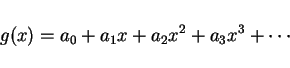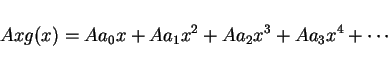

Next: 3 g(x)
Up: テイラー展開 その 2
Previous: 1 はじめに
(PDF ファイル: taylor3.pdf)
実はこのマクローリン展開は、一般二項展開公式
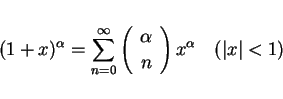 |
(1) |
さえ知っていれば「微分を使わずに」展開ができるのである。
ここで、
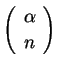 は、一般二項係数
は、一般二項係数
を意味する。
まず、 は展開すれば
は展開すれば
となるが、 はこれ自身多項式であり、関数の和のマクローリン展開は
マクローリン展開の和に等しいことを考えれば、
はこれ自身多項式であり、関数の和のマクローリン展開は
マクローリン展開の和に等しいことを考えれば、
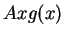 のマクローリン展開を求めてそれと足し算すればいいことが分かる。
また、
例えば
のマクローリン展開を求めてそれと足し算すればいいことが分かる。
また、
例えば 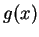 のマクローリン展開が
のマクローリン展開が
だったとすると、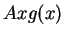 のマクローリン展開は、単にこの式の両辺に Ax を
かけたもの、すなわち
のマクローリン展開は、単にこの式の両辺に Ax を
かけたもの、すなわち
となるので、よって 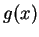 のマクローリン展開さえ求めればすむことになる。
のマクローリン展開さえ求めればすむことになる。


Next: 3 g(x)
Up: テイラー展開 その 2
Previous: 1 はじめに
Shigeharu TAKENO
2003年 11月 27日
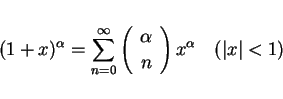
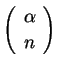 は、一般二項係数
は、一般二項係数
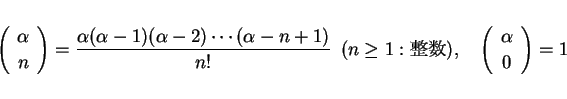
![]() は展開すれば
は展開すれば