3 考察
今、地球の中心を 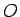 , 半径を
, 半径を 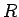 とし、
佐渡島の海岸を
とし、
佐渡島の海岸を 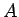 , そこから 30 km 離れた本州の海岸を
, そこから 30 km 離れた本州の海岸を 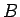 ,
,
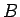 から佐渡島の海岸が見える高さ
から佐渡島の海岸が見える高さ 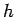 の地点を
の地点を 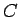 とし、
弧
とし、
弧 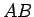 の中心角を
の中心角を 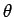 とする (図 1 参照)。
実際には、中心角
とする (図 1 参照)。
実際には、中心角 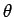 は非常に小さいので、
弧
は非常に小さいので、
弧 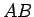 はほとんど直線と見てよく、よって弧
はほとんど直線と見てよく、よって弧 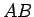 と弦
と弦 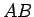 は違いはない。
よって、今弧
は違いはない。
よって、今弧 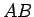 の長さが 30 km であるとする。
の長さが 30 km であるとする。
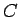 は
は 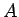 が見えるギリギリの高さなので、半径
が見えるギリギリの高さなので、半径 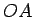 と
と 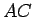 は垂直となり、
よって、
は垂直となり、
よって、
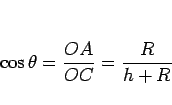
なので、
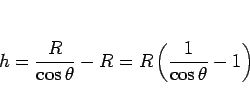 |
(1) |
となる。一方、弧 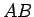 の長さが 30 km なので、
の長さが 30 km なので、
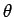 をラジアンで考えれば、
をラジアンで考えれば、
となり、よって
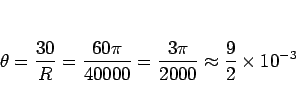 |
(4) |
である。
この最後の
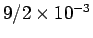 は、後で誤差評価で使用するもので、
直接近似値として使うわけではない。
は、後で誤差評価で使用するもので、
直接近似値として使うわけではない。
今、
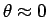 なので、
なので、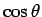 の
の 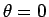 での
テイラー展開 (マクローリン展開) を考えれば、
での
テイラー展開 (マクローリン展開) を考えれば、
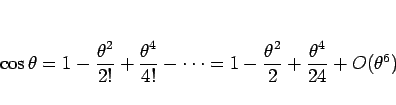
となる。ここで、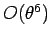 は、その部分が
は、その部分が 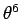 と
同じ位の大きさの値であることを意味するものとする。
と
同じ位の大きさの値であることを意味するものとする。
今、
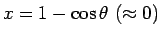 とすると、
とすると、
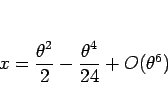
であり、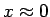 より
より 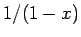 の
の 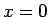 でのテイラー展開を考えれば、
でのテイラー展開を考えれば、
となる。(2) より 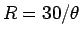 km なので、
(1), (5) より
km なので、
(1), (5) より
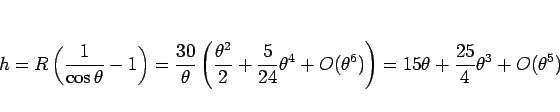
となる。この、
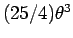 は (4) より
は (4) より
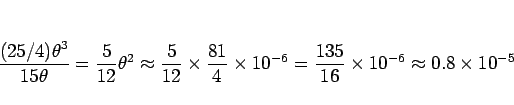
なので、
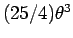 は
は 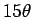 に比べてはるかに小さいこと
(10 万分の 1 程度) がわかる。
よって、(4) より
に比べてはるかに小さいこと
(10 万分の 1 程度) がわかる。
よって、(4) より
![\begin{displaymath}
h\approx 15\theta = 15\times \frac{3\pi}{2000} [\mathrm{km}]
= \frac{45}{2}\pi [\mathrm{m}]
\approx 70.7 [\mathrm{m}]
\end{displaymath}](img40.gif)
となる。
同様にして、最初から高次の項を無視して考えれば、
一般に 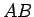 の距離が
の距離が 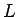 km の場合、
km の場合、
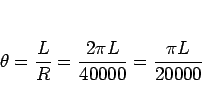
より、
![\begin{eqnarray*}h
&=&
R\left(\frac{1}{\cos\theta}-1\right)
=
R\left(\frac{1...
...i L^2}{40000} [\mathrm{km}]
=
\frac{\pi L^2}{40} [\mathrm{m}]\end{eqnarray*}](img43.gif)
という式が得られることになる。
角田山の高さは 482 m, 弥彦山は 688 m であるから、
いずれもその山腹からなら十分佐渡の海岸が見えることになるが、
シーサイドラインは、最も高いところでも 70 m はないような気がするので、
シーサイドラインからは佐渡の海岸は見えないように思う。
竹野茂治@新潟工科大学
2006年12月25日
![]() は
は ![]() が見えるギリギリの高さなので、半径
が見えるギリギリの高さなので、半径 ![]() と
と ![]() は垂直となり、
よって、
は垂直となり、
よって、
![]() なので、
なので、![]() の
の ![]() での
テイラー展開 (マクローリン展開) を考えれば、
での
テイラー展開 (マクローリン展開) を考えれば、
![]() とすると、
とすると、
![]() の距離が
の距離が ![]() km の場合、
km の場合、