6 証明その 3
次は、
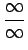 の形の不定形である
の形の不定形である
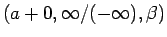 の
場合の証明を紹介する。
これは、4 節、5 節の証明とは
かなり異なる。
の
場合の証明を紹介する。
これは、4 節、5 節の証明とは
かなり異なる。
まず普通に思いつくのは、
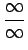 を
を
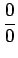 に変換することだろう。
すなわち、
に変換することだろう。
すなわち、
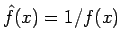 ,
,
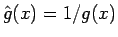 とすれば、
とすれば、
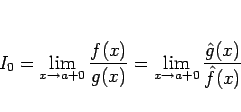
で、
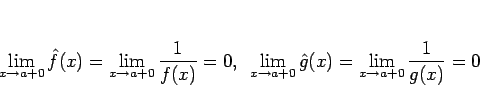
となって、
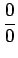 の形になる。
しかし、これで
の形になる。
しかし、これで
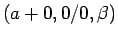 の結果を利用できるかというと、
必ずしもそうではない。
それは、
の結果を利用できるかというと、
必ずしもそうではない。
それは、
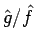 に対する
に対する 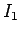 (これを
(これを 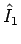 と書く) が、
と書く) が、
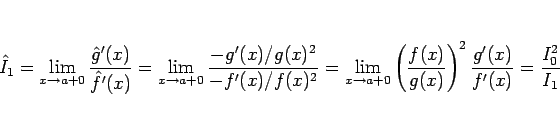
となり、
 の定理の仮定である
「
の定理の仮定である
「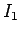 の存在」だけからは、この
の存在」だけからは、この 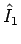 の存在が
保証できないために
の存在が
保証できないために
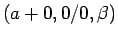 の定理を適用することが
できないからである。
の定理を適用することが
できないからである。
よって、このような置き換えではうまくいかないので、別の方法を考える。
今、
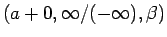 の場合の仮定は、
の場合の仮定は、
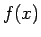 ,
, 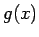 は
は 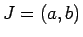 で連続、かつ微分可能で、
で連続、かつ微分可能で、
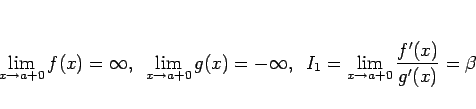 |
(5) |
となる。このとき、任意の 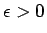 に対して、
に対して、
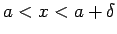 なるすべての
なるすべての 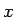 に対して
に対して
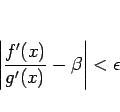
となるような 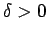 が取れる。
が取れる。
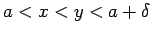 となる任意の
となる任意の 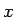 ,
, 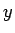 に対して、
コーシーの平均値の定理を適用すると、
ある
に対して、
コーシーの平均値の定理を適用すると、
ある 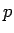 (
(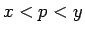 ) が存在して、
) が存在して、
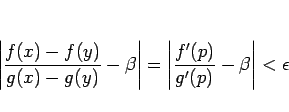 |
(6) |
となることは前と同じであるが、
今回は 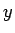 を、
を、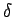 に対して
例えば
に対して
例えば 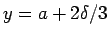 (
(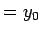 とする) と固定する。
この
とする) と固定する。
この 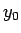 に対し、(5) を使えば、
に対し、(5) を使えば、
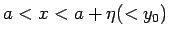 であるすべての
であるすべての 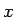 に対して
に対して
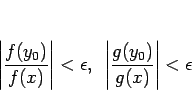 |
(7) |
となるような 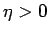 が取れる。
さらに、必要ならばより小さくすることで、
が取れる。
さらに、必要ならばより小さくすることで、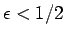 で
あると仮定してよい。
で
あると仮定してよい。
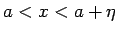 のとき、
のとき、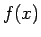 ,
, 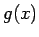 は、
(7) によりそれぞれ
は、
(7) によりそれぞれ 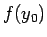 ,
, 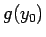 に
比べて絶対値は大きいので、
に
比べて絶対値は大きいので、
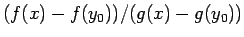 の値はほぼ
の値はほぼ 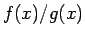 に近い値となる。
これは、以下のように変形すればよりよくわかる:
に近い値となる。
これは、以下のように変形すればよりよくわかる:
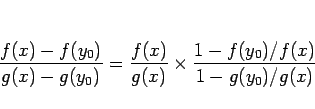
この後ろの分数の分子、分母にある分数は、
(7) によりその絶対値は少なくとも 1/2 より小さい。
(6) にこの後ろの分数の逆数をかけると、
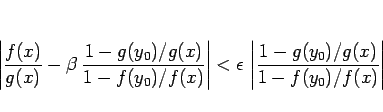 |
(8) |
となるが、(7) より、
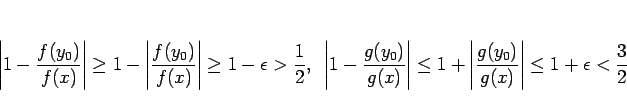
となるので、(8) より
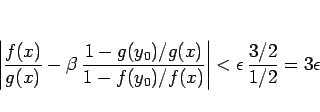 |
(9) |
となる。一方、(7) より、
となるので、
結局 (9), (10) より、
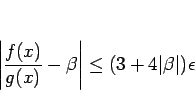
となることになる。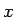 は
は 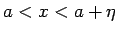 の任意の値、
の任意の値、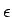 は
任意の値であったので、これは
は
任意の値であったので、これは 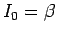 を意味する。
これで、
を意味する。
これで、
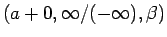 の場合のロピタルの定理が証明できた。
の場合のロピタルの定理が証明できた。
上の証明からわかる通り、これは
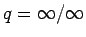 ,
,
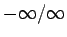 ,
,
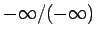 の場合でも全くこのまま通用するし、
また
の場合でも全くこのまま通用するし、
また 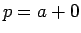 は
は 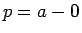 に簡単に置き換えることができ、
さらに
に簡単に置き換えることができ、
さらに 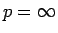 ,
, 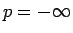 に関する証明に変えることも、
4 節の証明を 5 節で書き換えた
方法を用いれば可能になる。
に関する証明に変えることも、
4 節の証明を 5 節で書き換えた
方法を用いれば可能になる。
これで、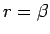 の場合の、
の場合の、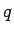 の
の 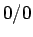 以外の 4 通りの場合で、
以外の 4 通りの場合で、
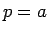 以外の 4 通り、すなわち合計 16 通りの証明が終わる。
以外の 4 通り、すなわち合計 16 通りの証明が終わる。
竹野茂治@新潟工科大学
2015年7月20日
![]() を
を
![]() に変換することだろう。
すなわち、
に変換することだろう。
すなわち、
![]() ,
,
![]() とすれば、
とすれば、
![]() の場合の仮定は、
の場合の仮定は、
![]() ,
, ![]() は
は ![]() で連続、かつ微分可能で、
で連続、かつ微分可能で、
![]() のとき、
のとき、![]() ,
, ![]() は、
(7) によりそれぞれ
は、
(7) によりそれぞれ ![]() ,
, ![]() に
比べて絶対値は大きいので、
に
比べて絶対値は大きいので、
![]() の値はほぼ
の値はほぼ ![]() に近い値となる。
これは、以下のように変形すればよりよくわかる:
に近い値となる。
これは、以下のように変形すればよりよくわかる:
![]() ,
,
![]() ,
,
![]() の場合でも全くこのまま通用するし、
また
の場合でも全くこのまま通用するし、
また ![]() は
は ![]() に簡単に置き換えることができ、
さらに
に簡単に置き換えることができ、
さらに ![]() ,
, ![]() に関する証明に変えることも、
4 節の証明を 5 節で書き換えた
方法を用いれば可能になる。
に関する証明に変えることも、
4 節の証明を 5 節で書き換えた
方法を用いれば可能になる。
![]() の場合の、
の場合の、![]() の
の ![]() 以外の 4 通りの場合で、
以外の 4 通りの場合で、
![]() 以外の 4 通り、すなわち合計 16 通りの証明が終わる。
以外の 4 通り、すなわち合計 16 通りの証明が終わる。