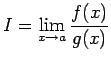 が
が
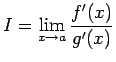 となる」
となる」
「が
か
の形 (不定形) であれば、
となる」
もう少しまともに書けば、以下の通り。
![]() ,
, ![]() が以下の条件を満たすとする。
が以下の条件を満たすとする。
(1)
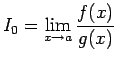 も
存在して、
も
存在して、
これは、条件 3 により
![]() の不定形の場合を
意味するが、「存在すれば」は
の不定形の場合を
意味するが、「存在すれば」は ![]() の方に対する条件であり、
そのとき
の方に対する条件であり、
そのとき ![]() が成り立つという定理であり、
通常の使い方とは実はむしろ逆である。例えば、
が成り立つという定理であり、
通常の使い方とは実はむしろ逆である。例えば、
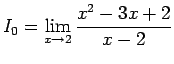 は
は
![]() の形なので、
普通は、
の形なので、
普通は、
「としなくてはならず、 つまり「となるので、
となる」
その辺は、普通は大目に見るのであるが、
できれば、本当は ![]() の存在が保証されて初めて「
の存在が保証されて初めて「![]() 」が
言えるということも頭に置いてもらいたい事実である。
例えば、以下の例では、
」が
言えるということも頭に置いてもらいたい事実である。
例えば、以下の例では、![]() は存在するが、
は存在するが、![]() は存在せず、
よって
は存在せず、
よって ![]() とはならない。
とはならない。
竹野茂治@新潟工科大学