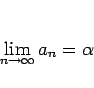次へ: 2 高校での極限の扱い 上へ: ε-δのお話 前へ: ε-δのお話 (PDF ファイル: epsdlt1.pdf)

1 はじめに

工学部に限らず、理学部数学科以外の大学の初年度の数学では、数列の極限

$$\lim_{n\rightarrow\infty}a_n=\alpha$$ (1)

や、関数の極限

$$\lim_{x\rightarrow a}f(x)=\beta$$ (2)

の厳密な定義を取り上げることはあまりないし、 またやるにしても定義を紹介するくらいで、 実際にその定義を使って何かを証明する、 ということはめったにやらないだろうと思う。 私が例年使用している工学部初年度向けの微積分の本にも 厳密な極限の定義は書かれていない。

しかし、理学部数学科ではそれ、すなわち、 いわゆる「$\varepsilon$-$\delta$ 論法」を使って 基本的な定理を証明するだけでなく、 具体的な問題を解くのにもそれを使うことがある。

工学部の学生であっても「極限」の考えはどのように厳密化されているのか、 ということが気になる人もいるかもしれないので、 少し、例もまじえてそれを紹介してみようと思う。

そこには、工学部の学生が普段目にする「式の取り扱い方」としての数学とは 少し違う、厳密さや論理性を追求した数学が見えてくる。 「$\varepsilon$-$\delta$ 論法」は、数学のそういう面を見るための 一つのよい例にもなっていると思う。

なお、この文章は参考文献 [1] に負うところが多い。 詳しい話を知りたい人は、[1] を参照するといいだろう。

次へ: 2 高校での極限の扱い 上へ: ε-δのお話 前へ: ε-δのお話