となる。 なお、この式の最初の 2 つの ex , e-x は、 それぞれ 1 回、2 回微分して元に戻るものになっている。 この (10) を示すことは、 実質的に 4 階の微分方程式
y = C1ex + C2e-x + C3cos x + C4sin x (10)
を解くことになるわけであるが、 しかし (10) を示すためには、まず
y(4) = y (11)
となる y が
y'' = - y (12)
となることを示すことが必要となる ((10) の後半部分) ので、まずこれを考える。 これは、5 節のように結果から定数を消す方法で考える。
y = C1cos x + C2sin x (13)
y がもし (13) であるとすると、
であるので、これを微分すれば、
= C1 + C2tan x
となって C1 が消え、この式を両辺 cos2x 倍して微分すれば、
= C2(tan x)' =
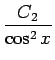
となって C2 も消えることになる。
cos2x
= 0
(14)
となるので、これを cos2x 倍すれば
=
=
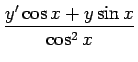
となる。この両辺を微分すると、
cos2x = y'cos x + y sin x
| = | (y'cos x + y sin x)' = y''cos x + y'(cos x)' + y'sin x + y(sin x)' | ||
| = | y''cos x - y'sin x + y'sin x + y cos x = (y'' + y)cos x | ||
となるから、両辺 cos2x で割って、
cos2x = C1
であるが、右辺は C1tan x の微分であるので、 左辺から右辺を引き算すれば、
=
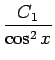
となるので、
- C1tan x
= 0
となる。よってこの両辺を cos x 倍すれば、
- C1tan x = C2
となって確かに (13) が得られることになる。
y = C1tan x cos x + C2cos x = C1sin x + C2cos x
そして、これを使えば、 4 回微分して元に戻るもの (11) の場合も容易に求めることができる。 まず、(11) の両辺に y'' を足せば、
であり、左辺は (y'' + y)'' に等しいので、 これは (y'' + y) が 2 回微分すると元に戻ることを意味し、 よって 4 節の結果により、
y(4) + y'' = y'' + y
であることがわかる。
y'' + y = C1ex + C2e-x (15)
一方、(11) の両辺から y'' を引けば、
となるので、 これは、(y'' - y) が (12) を満たすことを意味し、 よって (13) より、
y(4) - y'' = - y'' + y = - (y'' - y)
となる。 この (15) から (16) を引いて 2 で割れば、 結局
y'' - y = C3cos x + C4sin x (16)
となって (10) が得られることになる。
y =ex +
e-x -
cos x -
sin x
竹野茂治@新潟工科大学