|
|
(2) |
この公式は、形式的に以下のようにして導かれる。
[tf (t)](s) = -
[f (t)](s)
(2)
| - |
= | - |
|
| = | - |
を用いた。
f (x, y)dx =
(x, y)dx
(2) を繰り返せば一般に、
も得られる。 これにより、多項式倍のラプラス変換は、 ラプラス変換の微分で求まることになる。 これを用いれば、
[tkf (t)](s) = (- 1)k
[f (t)](s)
(3)
と求まる。
[t sin t] = -
[sin t]
= -
=
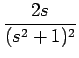
竹野茂治@新潟工科大学